Advertisements
Advertisements
प्रश्न
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
उत्तर
It is given that:
Mass of first block, m1 = 2 kg
Initial speed,v1 = 2.0 m/s
Mass of second block, m2 = 2 kg
Initial speed of this block = 0
For maximum possible loss in kinetic energy, we assume that the collision is elastic and both the blocks move with same final velocity v (say).
On applying the law of conservation of linear momentum, we get:
m1v1 + m2 ×0 = (m1+m2)v
2 × 2 = (2 + 2)v
⇒ v = 1 m/s
Loss in K.E. in elastic collision is give by,
\[= \frac{1}{2} m_1 v_1^2 - \frac{1}{2}\left( m_1 + m_2 \right)v\]
\[ = \left( \frac{1}{2} \right) \times 2 \times 2^2 - \left( \frac{1}{2} \right)(2 + 2) \times (1 )^2 \]
\[ = 4 - 2 = 2 J\]
\[(b) \text{ The actual loss in K . E . } = \frac{\text{ Maximum loss in K . E .}}{2} = 1 J\]
Let the final velocities of the blocks be v1 and v2 respectively. The coefficient of restitution is e.
\[\therefore\] The loss in K.E. is given by,
\[\left( \frac{1}{2} \right) \times 2 \times (2 )^2 - \left( \frac{1}{2} \right)2 \times v_1^2 - \left( \frac{1}{2} \right) \times 2 v_2^2 = 1\]
\[ \Rightarrow 4 - \left( v_1^2 + v_2^2 \right) = 1\]
\[ \Rightarrow 4 - \frac{\left( 1 + e^2 \right) \times 4}{2} = 1\]
\[ \Rightarrow 2\left( 1 + e^2 \right) = 3\]
\[ \Rightarrow 1 + e^2 = \frac{3}{2}\]
\[ \Rightarrow e^2 = \frac{1}{2}\]
\[ \Rightarrow e = \frac{1}{\sqrt{2}}\]
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 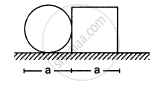
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
In an elastic collision
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.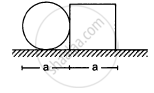
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
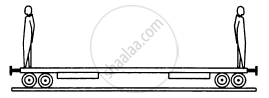
Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
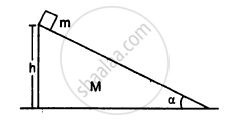
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
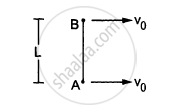
[Hint : The light rod will exert a force on the ball B
only along its length.]
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
In rotational motion of a rigid body, all particles move with ______.
Which of the following statements are correct?
For which of the following does the centre of mass lie outside the body?
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
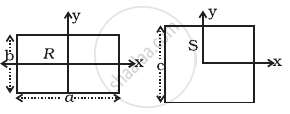
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
