Advertisements
Advertisements
प्रश्न
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
उत्तर
Given:
The mass of the both balls is m.
Initial speed of first ball = v
Initial speed of second ball = 0
Let the final of balls be v1 and v2 respectively.
\[e = \frac{\text{ velocity of separation}}{\text{ velocity of approach}}\]
\[ \Rightarrow e = \frac{v_1 - v_2}{v}\]
\[ \Rightarrow v_1 - v_2 = ev . . . \left( 1 \right)\]
On applying the law of conservation of linear momentum, we get:
\[m( v_1 + v_2 ) = mv \]
\[ \Rightarrow v_1 + v_2 = v . . . (2)\]
\[\text{ According to the given condition, }\]
\[\text{ Final K . E .} = \frac{3}{4} \text{ Initial K . E } . \]
\[ \Rightarrow \frac{1}{2}m v_1^2 + \frac{1}{2}m v_2^2 = \frac{3}{4} \times \frac{1}{2}m v^2 \]
\[ \Rightarrow v_1^2 + v_2^2 = \frac{3}{4} v^2 \]
\[ \Rightarrow \frac{( v_1 + v_2 )^2 + ( v_1 - v_2 )^2}{2} = \frac{3}{4} v^2 \]
\[ \Rightarrow \frac{\left( 1 + e^2 \right) v^2}{2} = \frac{3}{4} v^2 \left[ \text{ using the equations }\left( 1 \right) \text{ and } \left( 2 \right) \right]\]
\[ \Rightarrow 1 + e^2 = \left( \frac{3}{2} \right)\]
\[ \Rightarrow e^2 = \frac{1}{2}\]
\[ \Rightarrow e = \frac{1}{\sqrt{2}}\]
Hence, the coefficient of restitution is found to be\[\frac{1}{\sqrt{2}}\]
APPEARS IN
संबंधित प्रश्न
Two bodies make an elastic head-on collision on a smooth horizontal table kept in a car. Do you expect a change in the result if the car is accelerated in a horizontal road because of the non inertial character of the frame? Does the equation "Velocity of separation = Velocity of approach" remain valid in an accelerating car? Does the equation "final momentum = initial momentum" remain valid in the accelerating car?
If the total mechanical energy of a particle is zero, is its linear momentum necessarily zero? Is it necessarily nonzero?
Consider the situation of the previous problem. Take "the table plus the ball" as the system. friction between the table and the ball is then an internal force. As the ball slows down, the momentum of the system decreases. Which external force is responsible for this change in the momentum?
A van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in the forward direction. How can be persons sitting inside the van do it without coming out and pushing from behind?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A uranium-238 nucleus, initially at rest, emits an alpha particle with a speed of 1.4 × 107m/s. Calculate the recoil speed of the residual nucleus thorium-234. Assume that the mass of a nucleus is proportional to the mass number.
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.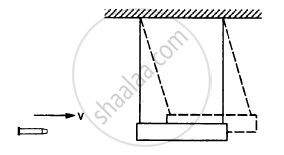
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
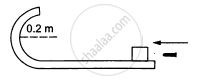
A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?
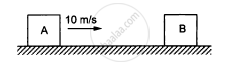
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

The following figure shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and the tangential accelerations of the centre when the ball is at A.
(c) Find the normal force and the frictional force acting on the if ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.

The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

