Advertisements
Advertisements
प्रश्न
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
विकल्प
\[\vec{v} , \vec{v}_1 \text{ and } \vec{v}_2\] must be parallel to each other.
None of the two of \[\vec{v} , \vec{v}_1 \text{ and } \vec{v}_2\] should be parallel to each other.
\[\vec{v_1} + \vec{v_2}\] must be parallel to \[\vec{v}\]
\[m_1 \vec{v_1} + m_2 \vec{v_2}\] must be parallel to \[\vec{v}\]
उत्तर
\[m_1 \vec{v_1} + m_2 \vec{v_2}\] must be parallel to \[\vec{v}\]
By the law of conservation of linear momentum, we can write:
\[\text{ Initial momentum } = \text{ Final momentum }\]
\[ \Rightarrow m \vec{v} = m_1 \vec{v}_1 + m_2 \vec{v}_2 \]
\[ \Rightarrow ( m_1 \vec{v}_1 + m_2 \vec{v}_2 ) \text{ must be parallel to } \vec{v}\]
APPEARS IN
संबंधित प्रश्न
A bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays at rest with respect to the car with the string making an angle θ with the vertical. The linear momentum of the bob as seen from the road is increasing with time. Is it a violation of conservation of linear momentum? If not, where is the external force changes the linear momentum?
Two bodies make an elastic head-on collision on a smooth horizontal table kept in a car. Do you expect a change in the result if the car is accelerated in a horizontal road because of the non inertial character of the frame? Does the equation "Velocity of separation = Velocity of approach" remain valid in an accelerating car? Does the equation "final momentum = initial momentum" remain valid in the accelerating car?
If the linear momentum of a particle is known, can you find its kinetic energy? If the kinetic energy of a particle is know can you find its linear momentum?
In one-dimensional elastic collision of equal masses, the velocities are interchanged. Can velocities in a one-dimensional collision be interchanged if the masses are not equal?
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
The quantities remaining constant in a collisions are
In an elastic collision
(a) the kinetic energy remains constant
(b) the linear momentum remains constant
(c) the final kinetic energy is equal to the initial kinetic energy
(d) the final linear momentum is equal to the initial linear momentum.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.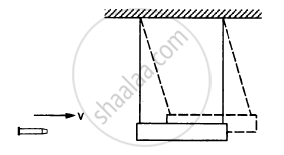
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
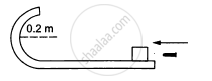
A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?
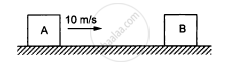
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
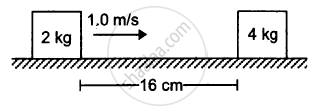
The friction coefficient between the horizontal surface and each of the block shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g = 10 m/s2.
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

