Advertisements
Advertisements
प्रश्न
A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
उत्तर
It is given that:
Mass of block, M = 200 g = 0.20 kg
Mass of the particle, m = 120 gm = 0.12 kg
Height of the particle, h = 45 cm = 0.45 m 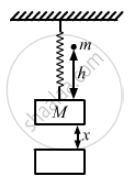
According to question, as the block attains equilibrium, the spring is stretched by a distance, x = 1.00 cm = 0.01 m.
i.e. M × g = K × x
⇒ 0.2 × g = K × x
⇒ 2 = K × 0.01
⇒ K = 200 N/m
The velocity with which the particle m strikes M is given by,
\[u = \sqrt{2gh}\]
\[u = \sqrt{2 \times 10 \times 0 . 45}\]
\[ = \sqrt{9} = 3 \text{ m/s}\]
After the collision, let the velocity of the particle and the block be V.
According to law of conservation of momentum, we can write:
mu = (m + M)V
Solving for V , we get:
\[V = \frac{0 . 12 \times 3}{0 . 32} = \frac{9}{8}\text{ m/s }\]
Let the spring be stretched through an extra deflection of δ.
On applying the law of conservation of energy, we can write:
Initial energy of the system before collision = Final energy of the system
\[\Rightarrow \frac{1}{2}m u^2 + \frac{1}{2}K x^2 = \frac{1}{2}\left( m + M \right) V^2 + \frac{1}{2}K \left( x + \delta \right)^2\]
Substituting appropriate values in the above equation, we get:
\[\left( \frac{1}{2} \right) \times 0 . 12 \times 9 + \left( \frac{1}{2} \right) \times 200 \times (0 . 01 )^2 = \left( \frac{1}{2} \right)0 . 32 \times \left( \frac{81}{64} \right) + \left( \frac{1}{2} \right) \times 200 \times (\delta + 0 . 1 )^2\]
On solving the above equation, we get:
δ = 0.061
m = 6.1 cm
APPEARS IN
संबंधित प्रश्न
Suppose we define a quantity 'Linear momentum' as linear momentum = mass × speed.
The linear momentum of a system of particles is the sum of linear momenta of the individual particles. Can we state principle of conservation of linear momentum as "linear momentum of a system remains constant if no external force acts on it"?
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
Consider the situation of the previous problem. Take "the table plus the ball" as the system. friction between the table and the ball is then an internal force. As the ball slows down, the momentum of the system decreases. Which external force is responsible for this change in the momentum?
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
The quantities remaining constant in a collisions are
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
In an elastic collision
(a) the kinetic energy remains constant
(b) the linear momentum remains constant
(c) the final kinetic energy is equal to the initial kinetic energy
(d) the final linear momentum is equal to the initial linear momentum.
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.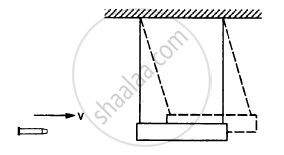
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
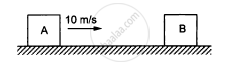
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

The following figure shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and the tangential accelerations of the centre when the ball is at A.
(c) Find the normal force and the frictional force acting on the if ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.

The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

