Advertisements
Advertisements
प्रश्न
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
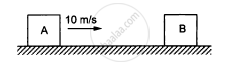
उत्तर
Given,
Speed of the block A = 10 m/s
The block B is kept at rest.
Coefficient of friction between the floor and block B, μ = 0.10
Let v1 and v2 be the velocities of A and B after collision, respectively.
(a) If the collision is perfectly elastic, linear momentum is conserved.
Using the law of conservation of linear momentum, we can write:
\[m u_1 + m u_2 = m v_1 + m v_2 \]
\[ \Rightarrow 10 + 0 = v_1 + v_2 \]
\[ v_1 + v_2 = 10 . . . \left( 1 \right)\]
\[\text{ We know,} \]
\[\text{ Velocity of separation } \left( \text{ after collision }\right) = \text{ Velocity of approach } \left( \text{ before collision } \right )\]
\[ v_1 - v_2 = - ( u_1 - v_2 )\]
\[ \Rightarrow v_1 - v_2 = - 10 . . . \left( 2 \right)\]
\[\text{ Substracting equation (2) from (1), we get: }\]
\[2 v_2 = 20\]
\[ \Rightarrow v_2 = 10 \text{ m/s }\]
The deceleration of block B is calculated as follows:
Applying the work-energy principle, we get:
\[\left( \frac{1}{2} \right) \times m \times (0 )^2 - \left( \frac{1}{2} \right) \times m \times v^2 = - m \times a \times s_1 \]
\[ \Rightarrow - \left( \frac{1}{2} \right) \times (10 )^2 = - \mu g \times s_1 \]
\[ \Rightarrow s_1 = \frac{100}{2 \times 0.1 \times 10} = 50 \text{ m }\]
(b) If the collision is perfectly inelastic, we can write:
\[m \times u_1 + m \times u_2 = (m + m) \times v\]
\[ \Rightarrow m \times 10 + m \times 0 = 2m \times v\]
\[ \Rightarrow v = \left( \frac{10}{2} \right) = 5 \text{ m/s }\]
The two blocks move together, sticking to each other.
∴ Applying the work-energy principle again, we get:
\[\left( \frac{1}{2} \right) \times 2m \times (0 )^2 - \left( \frac{1}{2} \right) \times 2m \times (v )^2 = 2m \times \mu g \times s_2 \]
\[ \Rightarrow \frac{(5 )^2}{0 . 1 \times 10 \times 2} = s_2 \]
\[ \Rightarrow s_2 = 12 . 5\]m
APPEARS IN
संबंधित प्रश्न
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
In an elastic collision
(a) the kinetic energy remains constant
(b) the linear momentum remains constant
(c) the final kinetic energy is equal to the initial kinetic energy
(d) the final linear momentum is equal to the initial linear momentum.
A ball hits a floor and rebounds after an inelastic collision. In this case
(a) the momentum of the ball just after the collision is same as that just before the collision
(b) the mechanical energy of the ball remains the same during the collision
(c) the total momentum of the ball and the earth is conserved
(d) the total energy of the ball and the earth remains the same
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
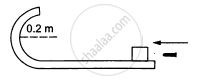
A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
A small disc is set rolling with a speed \[\nu\] on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
