Advertisements
Advertisements
प्रश्न
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
उत्तर
It is given that:
Mass of proton, mp = 1.67 × 10−27 kg
Momentum of electron = 1.4 × 10−26 kg m/s
Momentum of antineutrino = 6.4 × 10−27 kg m/s
Let the recoil speed of the proton be Vp.
(a) When the electron and the antineutrino are ejected in the same direction, and as the total momentum is conserved the proton should be ejected in opposite direction.
Applying the law of conservation of momentum, we get:
\[m_p V_p = p_{\text{electron }} + p_{\text{antineutrino }} \]
\[1 . 67 \times {10}^{- 27} \times V_P \]
\[= 1 . 4 \times {10}^{- 26} + 6 . 4 \times {10}^{- 27} \]
\[=20.4 \times 10^{- 27} \]
\[ \Rightarrow V_P = \left( \frac{20 . 4}{1 . 67} \right) = 12 . 2 \text{ m/s, in the opposite direction }\]
(b) When the electron and the antineutrino are ejected perpendicular to each other,
Total momentum of electron and antineutrino is given as,
\[p = \sqrt{p_{electron} + p_{antineutrino}} = \sqrt{(14 )^2 + (6 . 4 )^2} \times {10}^{- 27} = 15 . 4 \times {10}^{- 27} kg m/s\]
\[ \Rightarrow V_p = \frac{15 . 4 \times {10}^{- 27} \text{ kgm/s}}{1 . 67 \times {10}^{- 27} \text{ kg}}\]
\[ \Rightarrow V_p = 9 . 2 \text{m/s}\]
APPEARS IN
संबंधित प्रश्न
A bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays at rest with respect to the car with the string making an angle θ with the vertical. The linear momentum of the bob as seen from the road is increasing with time. Is it a violation of conservation of linear momentum? If not, where is the external force changes the linear momentum?
Two bodies make an elastic head-on collision on a smooth horizontal table kept in a car. Do you expect a change in the result if the car is accelerated in a horizontal road because of the non inertial character of the frame? Does the equation "Velocity of separation = Velocity of approach" remain valid in an accelerating car? Does the equation "final momentum = initial momentum" remain valid in the accelerating car?
Suppose we define a quantity 'Linear momentum' as linear momentum = mass × speed.
The linear momentum of a system of particles is the sum of linear momenta of the individual particles. Can we state principle of conservation of linear momentum as "linear momentum of a system remains constant if no external force acts on it"?
In one-dimensional elastic collision of equal masses, the velocities are interchanged. Can velocities in a one-dimensional collision be interchanged if the masses are not equal?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A shell is fired from a cannon with a velocity V at an angle θ with the horizontal direction. At the highest point in its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other piece immediately after the explosion is
A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
A block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s (In the following figure) towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
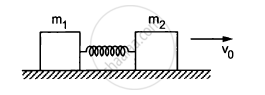
Two blocks of masses m1 and m2 are connected by a spring of spring constant k (See figure). The block of mass m2 is given a sharp impulse so that it acquires a velocity v0 towards right. Find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer.
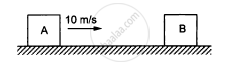
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
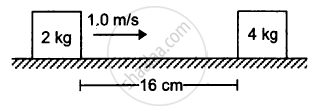
The friction coefficient between the horizontal surface and each of the block shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g = 10 m/s2.
A small disc is set rolling with a speed \[\nu\] on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
