Advertisements
Advertisements
प्रश्न
A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
उत्तर
It is given that:
Mass of the skater who is skating, m1 = 60 kg
Initial speed of this man, v1 = 10 m/s
Mass of the skater at rest, m2 = 40 kg
Initial speedof this man, v2 = 0
Let the velocity of both men after collision be v.
Using the law of conservation of momentum, we can write:
\[m_1 v_1 + m_2 v_2 = ( m_1 + m_2 )v\]
\[ \Rightarrow 60 \times 10 + 0 = 100 \times v\]
\[ \Rightarrow v = 6 \text{ m/s }\]
\[\text{ The loss in kinetic energy during collision is given as, }\]
\[ ∆ KE = \frac{1}{2} m_1 v_1^2 - \frac{1}{2}( m_1 + m_2 ) v^2 \]
\[ \Rightarrow ∆ KE = \frac{1}{2} \times 60 \times (10 )^2 - \frac{1}{2} \times 100 \times 36\]
\[ \Rightarrow ∆ KE = 1200 J\]
APPEARS IN
संबंधित प्रश्न
A bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays at rest with respect to the car with the string making an angle θ with the vertical. The linear momentum of the bob as seen from the road is increasing with time. Is it a violation of conservation of linear momentum? If not, where is the external force changes the linear momentum?
Two bodies make an elastic head-on collision on a smooth horizontal table kept in a car. Do you expect a change in the result if the car is accelerated in a horizontal road because of the non inertial character of the frame? Does the equation "Velocity of separation = Velocity of approach" remain valid in an accelerating car? Does the equation "final momentum = initial momentum" remain valid in the accelerating car?
If the total mechanical energy of a particle is zero, is its linear momentum necessarily zero? Is it necessarily nonzero?
If the linear momentum of a particle is known, can you find its kinetic energy? If the kinetic energy of a particle is know can you find its linear momentum?
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
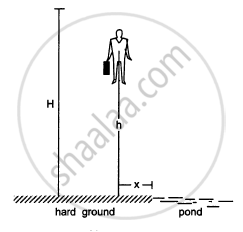
A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
Two friends A and B (each weighing 40 kg) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass 4 kg on the platform towards B which B catches. Then B rolls the ball towards A and A catches it. The ball keeps on moving back and forth between A and B. The ball has a fixed speed of 5 m/s on the platform. (a) Find the speed of A after he catches the ball for the first time. (c) Find the speeds of A and Bafter the all has made 5 round trips and is held by A. (d) How many times can A roll the ball? (e) Where is the centre of mass of the system "A + B + ball" at the end of the nth trip?
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
A small disc is set rolling with a speed \[\nu\] on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
