Advertisements
Advertisements
प्रश्न
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
उत्तर
It is given that:
Mass of the ball = 50 g =
\[0 . 05 \text{ Kg}\]
Speed of the ball, v = 2.0 m/s
Incident angle = 45˚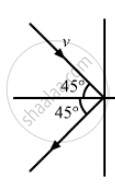
\[v = 2 \cos 45^\circ \hat i - 2 \sin 45^\circ \hat j \]
\[v' = - 2 \cos 45^\circ \hat i - 2 \sin 45^\circ \hat j\]
\[(a) \text{ Change in momentum } = m \vec{v} - m \vec{v} '\]
\[ = 0 . 05\left( 2 \cos 45^\circ\ \hat i - 2 \sin 45^\circ \hat j \right) - 0 . 05\left( - 2 \cos 45^\circ \hat i - 2 \sin 45^\circ \hat j \right)\]
\[ = 0 . 1 \cos 45^\circ\ \hat i - 0 . 1 \sin 45^\circ \ \hat j + 0 . 1 \cos 45^\circ \ \hat i + 0 . 1 \sin 45^\circ\ \hat j\]
\[ = 0 . 2 \cos 45^\circ\ \hat i \]
\[ \therefore \text{ Magnitude }= \frac{0 . 2}{\sqrt{2}} = 0 . 14 \text{ Kg m/s}\]
(b) The change in magnitude of the momentum of the ball,
\[\left| \vec{P}_2 \right| - \left| \vec{P}_1 \right| = 2 \times 0 . 5 - 2 \times 0 . 5 = 0\]
i.e. There is no change in magnitude of the momentum of the ball.
APPEARS IN
संबंधित प्रश्न
If the total mechanical energy of a particle is zero, is its linear momentum necessarily zero? Is it necessarily nonzero?
If the linear momentum of a particle is known, can you find its kinetic energy? If the kinetic energy of a particle is know can you find its linear momentum?
Suppose we define a quantity 'Linear momentum' as linear momentum = mass × speed.
The linear momentum of a system of particles is the sum of linear momenta of the individual particles. Can we state principle of conservation of linear momentum as "linear momentum of a system remains constant if no external force acts on it"?
Consider the situation of the previous problem. Take "the table plus the ball" as the system. friction between the table and the ball is then an internal force. As the ball slows down, the momentum of the system decreases. Which external force is responsible for this change in the momentum?
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
A shell is fired from a cannon with a velocity V at an angle θ with the horizontal direction. At the highest point in its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other piece immediately after the explosion is
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
A ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mass 1.0 kg. After the collision the balls stick together and remain motionless. What was the velocity of the 1.0 kg block before the collision?
A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
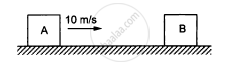
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
