Advertisements
Advertisements
प्रश्न
If the total mechanical energy of a particle is zero, is its linear momentum necessarily zero? Is it necessarily nonzero?
उत्तर
No. As the potential energy can have a negative value, the total energy of the system may sum up to zero.
For example:
Two masses A and B having masses 2 kg and 4 kg respectively move with a velocity of 4 ms-1 in opposite directions.
Kinetic energy of system (A and B)
\[= \frac{1}{2} \times 2 \times 4^2 + \frac{1}{2} \times 4 \times 4^2 \]
\[ = 48 J\]
If the gravitational potential energy of the system is −48 J, the total energy of the system will be zero. However, the linear momentum will be non-zero.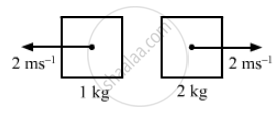
APPEARS IN
संबंधित प्रश्न
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
A van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in the forward direction. How can be persons sitting inside the van do it without coming out and pushing from behind?
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
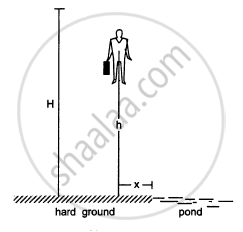
A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
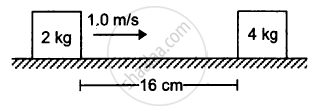
The friction coefficient between the horizontal surface and each of the block shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g = 10 m/s2.
A uniform rod pivoted at its upper end hangs vertically. It is displaced through an angle of 60° and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37° with the vertical.
A small disc is set rolling with a speed \[\nu\] on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
