Advertisements
Advertisements
प्रश्न
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
Advertisements
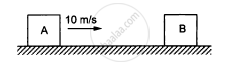
उत्तर
Given,
Speed of the block A = 10 m/s
The block B is kept at rest.
Coefficient of friction between the floor and block B, μ = 0.10
Let v1 and v2 be the velocities of A and B after collision, respectively.
(a) If the collision is perfectly elastic, linear momentum is conserved.
Using the law of conservation of linear momentum, we can write:
\[m u_1 + m u_2 = m v_1 + m v_2 \]
\[ \Rightarrow 10 + 0 = v_1 + v_2 \]
\[ v_1 + v_2 = 10 . . . \left( 1 \right)\]
\[\text{ We know,} \]
\[\text{ Velocity of separation } \left( \text{ after collision }\right) = \text{ Velocity of approach } \left( \text{ before collision } \right )\]
\[ v_1 - v_2 = - ( u_1 - v_2 )\]
\[ \Rightarrow v_1 - v_2 = - 10 . . . \left( 2 \right)\]
\[\text{ Substracting equation (2) from (1), we get: }\]
\[2 v_2 = 20\]
\[ \Rightarrow v_2 = 10 \text{ m/s }\]
The deceleration of block B is calculated as follows:
Applying the work-energy principle, we get:
\[\left( \frac{1}{2} \right) \times m \times (0 )^2 - \left( \frac{1}{2} \right) \times m \times v^2 = - m \times a \times s_1 \]
\[ \Rightarrow - \left( \frac{1}{2} \right) \times (10 )^2 = - \mu g \times s_1 \]
\[ \Rightarrow s_1 = \frac{100}{2 \times 0.1 \times 10} = 50 \text{ m }\]
(b) If the collision is perfectly inelastic, we can write:
\[m \times u_1 + m \times u_2 = (m + m) \times v\]
\[ \Rightarrow m \times 10 + m \times 0 = 2m \times v\]
\[ \Rightarrow v = \left( \frac{10}{2} \right) = 5 \text{ m/s }\]
The two blocks move together, sticking to each other.
∴ Applying the work-energy principle again, we get:
\[\left( \frac{1}{2} \right) \times 2m \times (0 )^2 - \left( \frac{1}{2} \right) \times 2m \times (v )^2 = 2m \times \mu g \times s_2 \]
\[ \Rightarrow \frac{(5 )^2}{0 . 1 \times 10 \times 2} = s_2 \]
\[ \Rightarrow s_2 = 12 . 5\]m
APPEARS IN
संबंधित प्रश्न
A bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays at rest with respect to the car with the string making an angle θ with the vertical. The linear momentum of the bob as seen from the road is increasing with time. Is it a violation of conservation of linear momentum? If not, where is the external force changes the linear momentum?
Two bodies make an elastic head-on collision on a smooth horizontal table kept in a car. Do you expect a change in the result if the car is accelerated in a horizontal road because of the non inertial character of the frame? Does the equation "Velocity of separation = Velocity of approach" remain valid in an accelerating car? Does the equation "final momentum = initial momentum" remain valid in the accelerating car?
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
The quantities remaining constant in a collisions are
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s (In the following figure) towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.
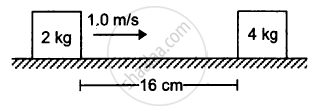
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
A small disc is set rolling with a speed \[\nu\] on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
The following figure shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and the tangential accelerations of the centre when the ball is at A.
(c) Find the normal force and the frictional force acting on the if ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.
The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?
