Advertisements
Advertisements
प्रश्न
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
उत्तर
It is given that:
Speed of the first particle during collision, \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]v
Let v' be the speed of the second particle, during collision.
On applying the law of conservation of linear momentum on both particles, we get:
m1u1 + m2u2 = m1v(t) + m2v'
\[\Rightarrow m_1 u_1 + m_2 u_2 = m_1 u_1 + m_1 \times \left( \frac{t}{∆ t} \right)( v_1 - u_1 ) + m_2 v'\]
\[\text{ On dividing both the sides by m} _2 , \text{ we get: }\]
\[ u_2 = \frac{m_1}{m_2}\left( \frac{t}{∆ t} \right)( v_1 - u_1 ) + v'\]
\[\Rightarrow v' = u_2 - \frac{m_1}{m_2}\left( \frac{t}{∆ t} \right)( v_1 - u_1 )\]
The speed of the second particle during collision can be written as a function of time and is given by the expression,\[u_2 - \frac{m_1}{m_2}\left( \frac{t}{∆ t} \right)( v_1 - u_1 )\] .
APPEARS IN
संबंधित प्रश्न
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
Consider the situation of the previous problem. Take "the table plus the ball" as the system. friction between the table and the ball is then an internal force. As the ball slows down, the momentum of the system decreases. Which external force is responsible for this change in the momentum?
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
A shell is fired from a cannon with a velocity V at an angle θ with the horizontal direction. At the highest point in its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other piece immediately after the explosion is
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
In an elastic collision
(a) the kinetic energy remains constant
(b) the linear momentum remains constant
(c) the final kinetic energy is equal to the initial kinetic energy
(d) the final linear momentum is equal to the initial linear momentum.
A man of mass 50 kg starts moving on the earth and acquires a speed 1.8 m/s. With what speed does the earth recoil? Mass of earth = 6 × 1024 kg.
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
Two friends A and B (each weighing 40 kg) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass 4 kg on the platform towards B which B catches. Then B rolls the ball towards A and A catches it. The ball keeps on moving back and forth between A and B. The ball has a fixed speed of 5 m/s on the platform. (a) Find the speed of A after he catches the ball for the first time. (c) Find the speeds of A and Bafter the all has made 5 round trips and is held by A. (d) How many times can A roll the ball? (e) Where is the centre of mass of the system "A + B + ball" at the end of the nth trip?
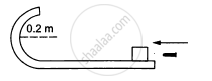
A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?
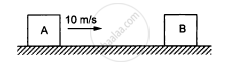
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
A uniform rod pivoted at its upper end hangs vertically. It is displaced through an angle of 60° and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37° with the vertical.
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

