Advertisements
Advertisements
प्रश्न
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
उत्तर
Let the mass of the rod and its angular velocity be m and ω (when hits the ground), respectively.
It is given that the rod has rotational motion only.
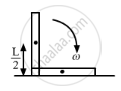
On applying the law of conservation of energy, we get
\[\frac{1}{2}I \omega^2 = mg\frac{l}{2}\]
\[ \Rightarrow \frac{m l^2}{3} \times \omega^2 = mgl\]
\[ \Rightarrow \omega^2 = \frac{3g}{l}\]
\[ \Rightarrow \omega = \sqrt{\frac{3g}{l}} = \sqrt{\left( 3 \times \frac{9 . 8}{1} \right)}\]
\[ \Rightarrow \omega = 5 . 42\text{ rad/s}\]
APPEARS IN
संबंधित प्रश्न
If the total mechanical energy of a particle is zero, is its linear momentum necessarily zero? Is it necessarily nonzero?
Suppose we define a quantity 'Linear momentum' as linear momentum = mass × speed.
The linear momentum of a system of particles is the sum of linear momenta of the individual particles. Can we state principle of conservation of linear momentum as "linear momentum of a system remains constant if no external force acts on it"?
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
A van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in the forward direction. How can be persons sitting inside the van do it without coming out and pushing from behind?
In one-dimensional elastic collision of equal masses, the velocities are interchanged. Can velocities in a one-dimensional collision be interchanged if the masses are not equal?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
Suppose the particle of the previous problem has a mass m and a speed \[\nu\] before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the centre of mass C of the system constituting "the rod plus the particle". (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision. (d) Find the angular momentum of the particle and of the rod about the centre of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. (f) Find the velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
A small disc is set rolling with a speed \[\nu\] on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
