Advertisements
Advertisements
प्रश्न
Suppose the particle of the previous problem has a mass m and a speed \[\nu\] before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the centre of mass C of the system constituting "the rod plus the particle". (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision. (d) Find the angular momentum of the particle and of the rod about the centre of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. (f) Find the velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
उत्तर
(a) It is given that no external torque and force is applied on the system.
Applying the law of conservation of momentum, we get
\[m\nu = \left( M + m \right) \nu'\]
\[\Rightarrow \nu' = \frac{m\nu}{M + m}\]
(b) Velocity of the particle w.r.t. centre of mass (COM) C before the collision = \[v_c = v - v'\]
\[\Rightarrow v_c = v - \frac{mv}{M + m} = \frac{Mv}{M + v}\]
(c) Velocity of the particle w.r.t. COM C before collision \[= - \frac{M\nu}{M + m}\]
(d) Distance of the COM from the particle,
\[x_{cm} = \frac{m_1 x_1 + m_2 x_2}{m_1 + m_2}\]
\[ \Rightarrow r = \frac{M \times \frac{L}{2} + m \times 0}{M + m}\]
\[ \Rightarrow r = \frac{ML}{2\left( M + m \right)}\]
∴ Angular momentum of body about COM
\[= mvr\]
\[ = m \times \frac{Mv}{\left( M + m \right)} \times \frac{ML}{2\left( M + m \right)}\]
\[ = \frac{M^2 mvL}{2 \left( M + m \right)^2}\]
∴ Angular momentum of rod about COM
\[= M \times \left( \frac{mv}{\left( M + m \right)} \right) \times \frac{1}{2}\frac{mL}{\left( M + m \right)}\]
\[ = \frac{M m^2 vL}{2 \left( M + m \right)^2}\]
(e) Moment of inertia about COM = I
\[= I_1 + I_2\]
\[I = m \left[ \frac{ML}{2\left( M + M \right)} \right]^2 + \frac{M L^2}{12} + M \left[ \frac{ML}{2\left( m + M \right)} \right]^2 \]
\[ = \frac{m M^2 L^2}{4 \left( m + M \right)^2} + \frac{M L^2}{12} + \frac{M m^2 L^2}{4 \left( M + m \right)^2}\]
\[ = \frac{3m M^2 L^2 + M \left( m + M \right)^2 L^2 + 3M m^2 L^2}{12 \left( m + M \right)^2}\]
\[ = \frac{M\left( M + 4m \right) L^2}{12\left( M + m \right)}\]
(f) About COM,
\[V_{cm} = \frac{m\nu}{M + m}\]
\[ \therefore I\omega = mvr = mv \times \frac{ML}{2 \left( M + m \right)}\]
\[ \Rightarrow \omega = \frac{m\nu ML}{2 \left( M + m \right)} \times \frac{12 \left( M + m \right)}{M \left( M + 4m \right) L^2}\]
\[= \frac{6m\nu}{\left( M + 4m \right)L}\]
APPEARS IN
संबंधित प्रश्न
If the linear momentum of a particle is known, can you find its kinetic energy? If the kinetic energy of a particle is know can you find its linear momentum?
Suppose we define a quantity 'Linear momentum' as linear momentum = mass × speed.
The linear momentum of a system of particles is the sum of linear momenta of the individual particles. Can we state principle of conservation of linear momentum as "linear momentum of a system remains constant if no external force acts on it"?
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
Consider the situation of the previous problem. Take "the table plus the ball" as the system. friction between the table and the ball is then an internal force. As the ball slows down, the momentum of the system decreases. Which external force is responsible for this change in the momentum?
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
A shell is fired from a cannon with a velocity V at an angle θ with the horizontal direction. At the highest point in its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other piece immediately after the explosion is
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
A man of mass 50 kg starts moving on the earth and acquires a speed 1.8 m/s. With what speed does the earth recoil? Mass of earth = 6 × 1024 kg.
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
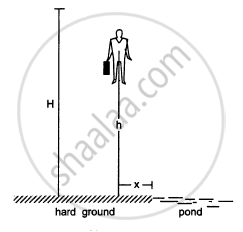
A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

