Advertisements
Advertisements
प्रश्न
The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

उत्तर
Given:
Mass of the block, A = m
Mass of the block, B = 2m
Let the initial velocity of block A be u1 and the final velocity of block A,when it reaches the block B be v1.
Using the work-energy theorem for block A, we can write:
Gain in kinetic energy = Loss in potential energy
`∴ (1/2)mv_1^2 - (1/2) m u_1^2 = mgh`
`Rightarrow v_1^2 - u_1^2 = 2gh`
`Rightarrow v_1= sqrt(2gh + u_1^2)` .......(1)
Let the block B just manages to reach the man's head.
i.e. the velocity of block B is zero at that point.
Again, applying the work-energy theorem for block B, we get:
`(1/2) xx 2m xx (0)^2 - (1/2 ) xx 2m xx v^2 = mgh`
`Rightarrow v = sqrt(2 gh)`
\[\text{ Therefore, before the collision }: \]
\[ \text{ Velocity of A, u}_A = v_1 \]
\[ \text{ Velocity of B, u}_B = 0\]
\[\text{ After the collision: }\]
\[ \text{ Velocity of A, v}_A = v (\text{ say })\]
\[\text{ Velocity of B, v}_B = \sqrt{2gh}\]
As the collision is elastic, K.E. and momentum are conserved.
\[m v_1 + 2m \times 0 = mv + 2m\sqrt{2gh}\]
\[ \Rightarrow v_1 - v = 2\sqrt{2gh} . . . \left( 2 \right)\]
\[\Rightarrow \left( \frac{1}{2} \right)m v_1^2 + \left( \frac{1}{2} \right)2m \times (0 )^2 = \left( \frac{1}{2} \right)m v^2 + \left( \frac{1}{2} \right)2m \left( \sqrt{2gh} \right)^2 \]
\[ \Rightarrow v_1^2 - v^2 = 2 \times \sqrt{2gh} \times \sqrt{2gh} . . . \left( 3 \right)\]
\[\text{ Dividing equation (3) by equation (2), we get: } \]
\[ v_1 + v = \sqrt{2gh} . . . \left( 4 \right)\]
\[\text{ Adding the equations } \left( 4 \right) \text{ and } \left( 2 \right), \text{ we get: } \]
\[2 v_1 = 3\sqrt{2gh}\]
\[\text{ Now using equation } \left( 1 \right) \text{ to substitue the value of v}_1 , \text{ we get: }\]
\[\sqrt{2gh + u^2} = \left( \frac{3}{2} \right)\sqrt{2gh}\]
\[ \Rightarrow 2gh + u^2 = \left( \frac{9}{4} \right)(2gh)\]
\[ \Rightarrow u = \sqrt{2 . 5 gh}\]
Block a should be started with a minimum velocity of \[\sqrt{2 . 5gh}\]
to get the sleeping man awakened.
APPEARS IN
संबंधित प्रश्न
If the total mechanical energy of a particle is zero, is its linear momentum necessarily zero? Is it necessarily nonzero?
Suppose we define a quantity 'Linear momentum' as linear momentum = mass × speed.
The linear momentum of a system of particles is the sum of linear momenta of the individual particles. Can we state principle of conservation of linear momentum as "linear momentum of a system remains constant if no external force acts on it"?
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
A man of mass 50 kg starts moving on the earth and acquires a speed 1.8 m/s. With what speed does the earth recoil? Mass of earth = 6 × 1024 kg.
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.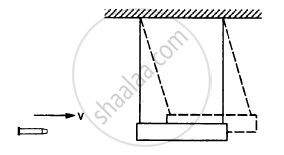
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
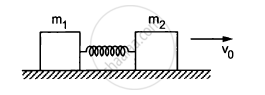
Two blocks of masses m1 and m2 are connected by a spring of spring constant k (See figure). The block of mass m2 is given a sharp impulse so that it acquires a velocity v0 towards right. Find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer.
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
A small disc is set rolling with a speed \[\nu\] on the horizontal part of the track of the previous problem from right to left. To what height will it climb up the curved part?
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
