Advertisements
Advertisements
प्रश्न
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
उत्तर
Given:
The mass of the both balls is m.
Initial speed of first ball = v
Initial speed of second ball = 0
Let the final of balls be v1 and v2 respectively.
On applying the law of conservation of linear momentum, we get:
Hence, the coefficient of restitution is found to be
APPEARS IN
संबंधित प्रश्न
If the linear momentum of a particle is known, can you find its kinetic energy? If the kinetic energy of a particle is know can you find its linear momentum?
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
In one-dimensional elastic collision of equal masses, the velocities are interchanged. Can velocities in a one-dimensional collision be interchanged if the masses are not equal?
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
The quantities remaining constant in a collisions are
A nucleus moving with a velocity
A shell is fired from a cannon with a velocity V at an angle θ with the horizontal direction. At the highest point in its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other piece immediately after the explosion is
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.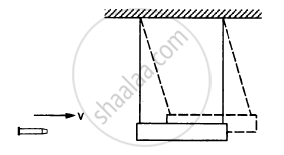
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
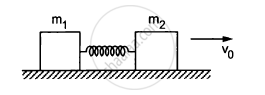
Two blocks of masses m1 and m2 are connected by a spring of spring constant k (See figure). The block of mass m2 is given a sharp impulse so that it acquires a velocity v0 towards right. Find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer.
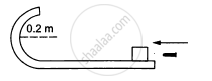
A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
The following figure shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and the tangential accelerations of the centre when the ball is at A.
(c) Find the normal force and the frictional force acting on the if ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.

A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
