Advertisements
Advertisements
Question
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
Solution
Given:
The mass of the both balls is m.
Initial speed of first ball = v
Initial speed of second ball = 0
Let the final of balls be v1 and v2 respectively.
\[e = \frac{\text{ velocity of separation}}{\text{ velocity of approach}}\]
\[ \Rightarrow e = \frac{v_1 - v_2}{v}\]
\[ \Rightarrow v_1 - v_2 = ev . . . \left( 1 \right)\]
On applying the law of conservation of linear momentum, we get:
\[m( v_1 + v_2 ) = mv \]
\[ \Rightarrow v_1 + v_2 = v . . . (2)\]
\[\text{ According to the given condition, }\]
\[\text{ Final K . E .} = \frac{3}{4} \text{ Initial K . E } . \]
\[ \Rightarrow \frac{1}{2}m v_1^2 + \frac{1}{2}m v_2^2 = \frac{3}{4} \times \frac{1}{2}m v^2 \]
\[ \Rightarrow v_1^2 + v_2^2 = \frac{3}{4} v^2 \]
\[ \Rightarrow \frac{( v_1 + v_2 )^2 + ( v_1 - v_2 )^2}{2} = \frac{3}{4} v^2 \]
\[ \Rightarrow \frac{\left( 1 + e^2 \right) v^2}{2} = \frac{3}{4} v^2 \left[ \text{ using the equations }\left( 1 \right) \text{ and } \left( 2 \right) \right]\]
\[ \Rightarrow 1 + e^2 = \left( \frac{3}{2} \right)\]
\[ \Rightarrow e^2 = \frac{1}{2}\]
\[ \Rightarrow e = \frac{1}{\sqrt{2}}\]
Hence, the coefficient of restitution is found to be\[\frac{1}{\sqrt{2}}\]
APPEARS IN
RELATED QUESTIONS
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
A van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in the forward direction. How can be persons sitting inside the van do it without coming out and pushing from behind?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
Internal forces can change
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
A man of mass 50 kg starts moving on the earth and acquires a speed 1.8 m/s. With what speed does the earth recoil? Mass of earth = 6 × 1024 kg.
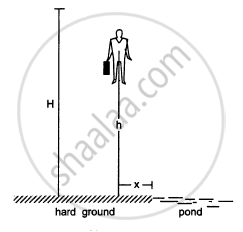
A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
A ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mass 1.0 kg. After the collision the balls stick together and remain motionless. What was the velocity of the 1.0 kg block before the collision?
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
Two friends A and B (each weighing 40 kg) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass 4 kg on the platform towards B which B catches. Then B rolls the ball towards A and A catches it. The ball keeps on moving back and forth between A and B. The ball has a fixed speed of 5 m/s on the platform. (a) Find the speed of A after he catches the ball for the first time. (c) Find the speeds of A and Bafter the all has made 5 round trips and is held by A. (d) How many times can A roll the ball? (e) Where is the centre of mass of the system "A + B + ball" at the end of the nth trip?
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.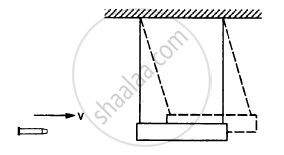
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
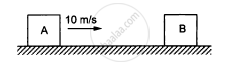
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

The following figure shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and the tangential accelerations of the centre when the ball is at A.
(c) Find the normal force and the frictional force acting on the if ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.

