Advertisements
Advertisements
Question
A ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mass 1.0 kg. After the collision the balls stick together and remain motionless. What was the velocity of the 1.0 kg block before the collision?
Solution
It is given that:
Speed of the ball, v1 = 5.0 m/s
Mass of the ball, m1 = 0.5 kg
Mass of another ball, m2 = 1 kg
Let the velocity of this ball be v2 m/s.
On applying the law of conservation of momentum, we get:
\[m_1 v_1 + m_2 v_2 = 0\]
\[0 . 5 \times 5 + 1 \times v_2 = 0\]
\[ \Rightarrow v_2 = - 2 . 5 \text{ m/s }\]
Hence, the velocity of second ball is 2.5 m/s, opposite to the direction of motion of the first ball.
APPEARS IN
RELATED QUESTIONS
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
A van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in the forward direction. How can be persons sitting inside the van do it without coming out and pushing from behind?
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
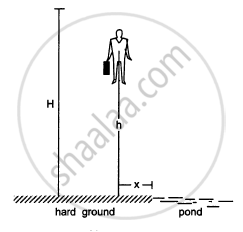
A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
In a typical Indian Bugghi (a luxury cart drawn by horses), a wooden plate is fixed on the rear on which one person can sit. A bugghi of mass 200 kg is moving at a speed of 10 km/h. As it overtakes a school boy walking at a speed of 4 km/h, the boy sits on the wooden plate. If the mass of the boy is 25 kg, what will be the plate. If the mass of the boy is 25 kg, what will be the new velocity of the bugghi ?
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.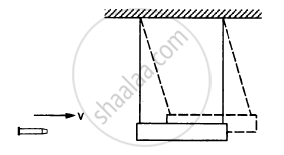
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
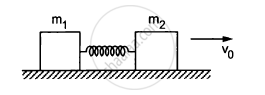
Two blocks of masses m1 and m2 are connected by a spring of spring constant k (See figure). The block of mass m2 is given a sharp impulse so that it acquires a velocity v0 towards right. Find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer.
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

