Advertisements
Advertisements
Question
A block of mass 200 g is suspended through a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g = 10 m/s2.
Solution
It is given that:
Mass of block, M = 200 g = 0.20 kg
Mass of the particle, m = 120 gm = 0.12 kg
Height of the particle, h = 45 cm = 0.45 m 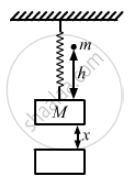
According to question, as the block attains equilibrium, the spring is stretched by a distance, x = 1.00 cm = 0.01 m.
i.e. M × g = K × x
⇒ 0.2 × g = K × x
⇒ 2 = K × 0.01
⇒ K = 200 N/m
The velocity with which the particle m strikes M is given by,
\[u = \sqrt{2gh}\]
\[u = \sqrt{2 \times 10 \times 0 . 45}\]
\[ = \sqrt{9} = 3 \text{ m/s}\]
After the collision, let the velocity of the particle and the block be V.
According to law of conservation of momentum, we can write:
mu = (m + M)V
Solving for V , we get:
\[V = \frac{0 . 12 \times 3}{0 . 32} = \frac{9}{8}\text{ m/s }\]
Let the spring be stretched through an extra deflection of δ.
On applying the law of conservation of energy, we can write:
Initial energy of the system before collision = Final energy of the system
\[\Rightarrow \frac{1}{2}m u^2 + \frac{1}{2}K x^2 = \frac{1}{2}\left( m + M \right) V^2 + \frac{1}{2}K \left( x + \delta \right)^2\]
Substituting appropriate values in the above equation, we get:
\[\left( \frac{1}{2} \right) \times 0 . 12 \times 9 + \left( \frac{1}{2} \right) \times 200 \times (0 . 01 )^2 = \left( \frac{1}{2} \right)0 . 32 \times \left( \frac{81}{64} \right) + \left( \frac{1}{2} \right) \times 200 \times (\delta + 0 . 1 )^2\]
On solving the above equation, we get:
δ = 0.061
m = 6.1 cm
APPEARS IN
RELATED QUESTIONS
If the linear momentum of a particle is known, can you find its kinetic energy? If the kinetic energy of a particle is know can you find its linear momentum?
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
A van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in the forward direction. How can be persons sitting inside the van do it without coming out and pushing from behind?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
A ball hits a floor and rebounds after an inelastic collision. In this case
(a) the momentum of the ball just after the collision is same as that just before the collision
(b) the mechanical energy of the ball remains the same during the collision
(c) the total momentum of the ball and the earth is conserved
(d) the total energy of the ball and the earth remains the same
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
A ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mass 1.0 kg. After the collision the balls stick together and remain motionless. What was the velocity of the 1.0 kg block before the collision?
A 60 kg man skating with a speed of 10 m/s collides with a 40 kg skater at rest and they cling to each other. Find the loss of kinetic energy during the collision.
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
A block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s (In the following figure) towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
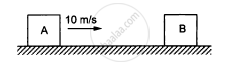
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
Suppose the particle of the previous problem has a mass m and a speed \[\nu\] before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the centre of mass C of the system constituting "the rod plus the particle". (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision. (d) Find the angular momentum of the particle and of the rod about the centre of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. (f) Find the velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
A metre stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
A uniform rod pivoted at its upper end hangs vertically. It is displaced through an angle of 60° and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37° with the vertical.
A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
