Advertisements
Advertisements
Question
A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?
Advertisements
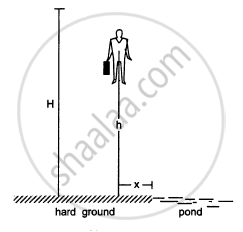
Solution
Mass of man = M
Initial velocity of the man = 0
Mass of bag = m
Let the man throws the bag towards left with a velocity v and himself moves towards right with a velocity V.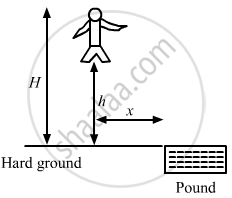
Using the law of conservation of momentum,
\[mv = MV\]
\[ \Rightarrow v = \frac{MV}{m} . . . (1)\]
\[\text{ Let the total time he takes to reach ground be t_1 . }\]
\[ \Rightarrow t_1 = \sqrt{\frac{2H}{g}}\]
\[\text{ Let the total time he takes to reach the height h be t_2 .} \]
\[ \Rightarrow t_2 = \sqrt{\frac{2(H - h)}{g}}\]
\[ \therefore \text{ The time of flying in covering the remaining height h is,} \]
\[ t = t_1 - t_2 \]
\[ \Rightarrow t = \sqrt{\frac{2H}{g}} - \sqrt{\frac{2(H - h)}{g}}\]
\[ = \sqrt{\frac{2}{g}}\left( \sqrt{H} - \sqrt{H - h} \right)\]
During this time, the man covers a horizontal distance x and lands in the water.
\[\Rightarrow x = V \times t\]
\[ \Rightarrow V = \frac{x}{t}\]
\[ \therefore v = \frac{M}{m}\frac{x}{t} \left[ \text{ using equation } \left( 1 \right) \right]\]
\[ = \frac{M}{m}\frac{x}{\sqrt{\frac{2}{g}}\left( \sqrt{H} - \sqrt{H - h} \right)}\]
Thus, the minimum horizontal velocity imparted to the bag, such that the man lands in the water is
\[\frac{M}{m}\frac{x}{\sqrt{\frac{2}{g}}\left( \sqrt{H} - \sqrt{H - h} \right)}\]
Let the bag lands at a distance x' towards left from actual line of fall.
As there is no external force in horizontal direction, the x-coordinate of the centre of mass will remain same.
\[\Rightarrow 0 = \frac{M \times (x) + m \times x'}{M + m}\]
\[ \Rightarrow x' = - \frac{M}{m}x\]
Therefore, the bag will land at a distance
\[\frac{M}{m}x\]
APPEARS IN
RELATED QUESTIONS
A bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays at rest with respect to the car with the string making an angle θ with the vertical. The linear momentum of the bob as seen from the road is increasing with time. Is it a violation of conservation of linear momentum? If not, where is the external force changes the linear momentum?
Use the definition of linear momentum from the previous question. Can we state the principle of conservation of linear momentum for a single particle?
A van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in the forward direction. How can be persons sitting inside the van do it without coming out and pushing from behind?
Internal forces can change
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
In an elastic collision
(a) the kinetic energy remains constant
(b) the linear momentum remains constant
(c) the final kinetic energy is equal to the initial kinetic energy
(d) the final linear momentum is equal to the initial linear momentum.
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
A gun is mounted on a railroad car. The mass of the car, the gun, the shells and the operator is 50 m where m is the mass of one shell. If the velocity of the shell with respect to the gun (in its state before firing) is 200 m/s, what is the recoil speed of the car after the second shot? Neglect friction.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
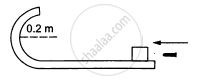
A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
Two blocks of masses m1 and m2 are connected by a spring of spring constant k (See figure). The block of mass m2 is given a sharp impulse so that it acquires a velocity v0 towards right. Find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer.
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
Suppose the particle of the previous problem has a mass m and a speed \[\nu\] before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the centre of mass C of the system constituting "the rod plus the particle". (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision. (d) Find the angular momentum of the particle and of the rod about the centre of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. (f) Find the velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.
