Advertisements
Advertisements
Question
A small block of superdense material has a mass of 3 × 1024kg. It is situated at a height h (much smaller than the earth's radius) from where it falls on the earth's surface. Find its speed when its height from the earth's surface has reduce to to h/2. The mass of the earth is 6 × 1024kg.
Solution
It is given that h is much lesser than the radius of the earth.
Mass of the earth, Me = 6 × 1024 kg
Mass of the block, Mb = 3 × 1024 kg
Let Ve be the velocity of the earth and Vb be the velocity of the block.
Let the earth and the block be attracted by gravitational force.
Thus, according to the conservation law of energy, the change in gravitational potential energy will be the K.E. of the block.
`GM_eM_b(1/(R + (h/2)) - 1/(R + h)) = (1/2)M_e xx V_e^2 + (1/2)M_b xx V_b^2` ...(i)
The momentum is conserved as only the internal force acts in this system.
MeVe = MbVb
⇒ `V_e = (M_bV_b)/M_e` ...(ii)
Putting in equation (i),
`GM_eM_b[2/(2R + h) - 1/(R + h)]`
= `(1/2) xx M_e^2 xx (M_b^2V_b^2)/M_e^2 + (1/2) xx M_b xx V_b^2`
= `(1/2) xx V_b^2 M_b/M_e + 1/2 xx M_b xx V_b^2`
⇒ `GM_e (2r + 2h - 2R - h)/((2R + h)(R + h))`
= `(1/2) xx V_b^2 xx ((3 xx 10^24)/(6 xx 10^24) + 1)`
⇒ `[(GM xx h)/(2R^2)] = (1/2) xx V_b^2 xx (3/2)`
⇒ `gh = V_b^2 xx (3/2)`
`V_b = (2gh)/3`
APPEARS IN
RELATED QUESTIONS
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
Consider the following two statements:
(A) The linear momentum of a particle is independent of the frame of reference.
(B) The kinetic energy of a particle is independent of the frame of reference.
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
The quantities remaining constant in a collisions are
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A man of mass 50 kg starts moving on the earth and acquires a speed 1.8 m/s. With what speed does the earth recoil? Mass of earth = 6 × 1024 kg.
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s (In the following figure) towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

A bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bullet emerges with a speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction coefficient between the block and the surface (See figure).
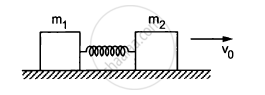
Two blocks of masses m1 and m2 are connected by a spring of spring constant k (See figure). The block of mass m2 is given a sharp impulse so that it acquires a velocity v0 towards right. Find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer.
Suppose the particle of the previous problem has a mass m and a speed \[\nu\] before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the centre of mass C of the system constituting "the rod plus the particle". (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision. (d) Find the angular momentum of the particle and of the rod about the centre of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. (f) Find the velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
