Advertisements
Advertisements
Question
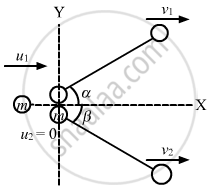
A body of mass m makes an elastic collision with another identical body at rest. Show that if the collision is not head-on the bodies go at right angle to each other after the collision.
Solution
According to the question, the collision of the two bodies of mass m is not head-on. Thus, the two bodies move in different directions.
Let the velocity vectors of the two bodies after collision be v1 and v2.
As the collision in the question is elastic, momentum is conserved.
On applying the law of conservation of momentum in X-direction, we get:
\[m u_1 + m \times 0 = m v_1 \cos \alpha + m v_2 \cos \beta . . . (i)\]
On applying the law of conservation of momentum in Y-direction, we get:
\[0 = m v_1 \sin \alpha - m v_2 \sin \beta . . . (ii)\]
\[ \Rightarrow m v_1 \sin \alpha = m v_2 \sin \beta\]
\[\text{ Now }, \]
\[\left( \frac{1}{2} \right)m u_1^2 + 0 = \left( \frac{1}{2} \right)m v_1^2 + \left( \frac{1}{2} \right)m \times v_2^2 \]
\[ \Rightarrow u_1^2 = v_1^2 + v_2^2 . . . (iii)\]
\[\text{ On squaring equation (i), we get: }\]
\[ u_1^2 = v_1^2 \cos^2 \alpha + v_2^2 \cos^2 \beta + 2 v_1 v_2 \cos \alpha \cos \beta\]
\[\text{ Equating the equations (i) and (iii), we get }\]
\[ v_1^2 + v_2^2 = v_1^2 \cos^2 \alpha + v_2^2 \cos^2 \beta + 2 v_1 v_2 \cos \alpha \cos \beta\]
\[ \Rightarrow {v_1}^2 \sin^2 \alpha + {v_2}^2 \sin^2 \beta = 2 v_1 v_2 \cos \alpha \cos \beta\]
\[ \Rightarrow 2 {v_1}^2 \sin^2 \alpha = 2 \times v_1 \times \frac{v_1 \sin \alpha}{\sin \beta} \cos \alpha \cos \beta\]
\[ \Rightarrow \sin \alpha \sin \beta = \cos \alpha \cos \beta\]
\[ \Rightarrow \cos \alpha . \cos \beta - \sin \alpha \cos \beta = 0\]
\[ \Rightarrow \cos (\alpha + \beta) = 0 = \cos 90^\circ\]
\[ \Rightarrow \alpha + \beta = 90^\circ\]
APPEARS IN
RELATED QUESTIONS
Can the centre of mass of a body be at a point outside the body?
The weight Mg of an extended body is generally shown in a diagram to act through the centre of mass. Does it mean that the earth does not attract other particles?
All the particles of a body are situated at a distance R from the origin. The distance of the centre of mass of the body from the origin is
A body falling vertically downwards under gravity breaks in two parts of unequal masses. The centre of mass of the two parts taken together shifts horizontally towards
A body at rest breaks into two pieces of equal masses. The parts will move
A body moving towards a finite body at rest collides with it. It is possible that
(a) both the bodies come to rest
(b) both the bodies move after collision
(c) the moving body comes to rest and the stationary body starts moving
(d) the stationary body remains stationary, the moving body changes its velocity.
In a head-on elastic collision of two bodies of equal masses
(a) the velocities are interchanged
(b) the speeds are interchanged
(c) the momenta are interchanged
(d) the faster body slows down and the slower body speeds up.
A block at rest explodes into three equal parts. Two parts start moving along X and Y axes respectively with equal speeds of 10 m/s. Find the initial velocity of the third part.
When tall building are constructed on earth, the duration of day-night slightly increases. Is it true?
A small particle travelling with a velocity v collides elastically with a spherical body of equal mass and of radius r initially kept at rest. The centre of this spherical body is located a distance ρ(< r) away from the direction of motion of the particle (see figure below). Find the final velocities of the two particles.
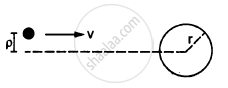
[Hint : The force acts along the normal to the sphere
through the contact. Treat the collision as onedimensional
for this direction. In the tangential direction no force acts and the velocities do not change].
Figure shows a small body of mass m placed over a larger mass M whose surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed v and the system is left to itself. Assume that all the surface are frictionless. (a) Find the speed of the larger block when the smaller block is sliding on the vertical part. (b) Find the speed of the smaller mass when it breaks off the larger mass at height h. (c) Find the maximum height (from the ground) that the smaller mass ascends. (d) Show that the smaller mass will again land on the bigger one. Find the distance traversed by the bigger block during the time when the smaller block was in its flight under gravity.

Two bodies of mass 1 kg and 3 kg have position vectors `hati + 2hatj + hatk` and `-3hati - 2hatj + hatk` respectively. The magnitude of position vector of centre of mass of this system will be similar to the magnitude of vector ______.
