Advertisements
Advertisements
Question
A bullet of mass 10 g moving horizontally at a speed of 50√7 m/s strikes a block of mass 490 g kept on a frictionless track as shown in figure. The bullet remains inside the block and the system proceeds towards the semicircular track of radius 0.2 m. Where will the block strike the horizontal part after leaving the semicircular track?
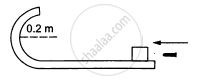
Solution
Given:
Mass of block = 490 gm
Initial speed of the block = 0
Mass of bullet = 10 gm
Initial speed of the bullet, v1 = \[50\sqrt{7} m/s\]
As the bullet gets embedded inside the block, this is an example of a perfectly inelastic collision.
Let the final velocity of the system (block and bullet) be VA.
Using the law of conservation of linear momentum, we get:
m1 + m2 × 0 = ( m1 + m2 ) VA
⇒10 × 10 - 3 × 507 + 490 × 10 - 3 × 0 = (490 + 10) × 10 - 3 × vA
∴ vA= \[\sqrt{7}\]
When the block loses contact at D, the component mg acts on it. Let the velocity at D be vB.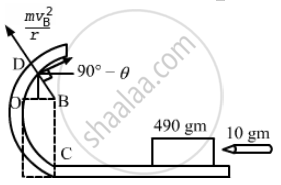
\[\frac{m( v_B )^2}{r} = mg\sin\theta\]
\[( v_B )^2 = gr \sin\theta . . . (1)\]
Using work energy theorem
\[\left( \frac{1}{2} \right)m v_B^2 - \left( \frac{1}{2} \right)m v_A^2 = - mg(0 . 2 + 0 . 2\sin\theta)\]
\[\left( \frac{1}{2} \right)gr\sin\theta - \left( \frac{1}{2} \right) \left( \sqrt{7} \right)^2 = g(0 . 2 + 0 . 2\sin\theta)\]
\[3 . 5 - \frac{1}{2} + 9 . 8 + 0 . 2 + \sin\theta = 9 . 8 + 0 . 2 (1 + \sin\theta)\]
\[3 . 5 - 0 . 98 \sin\theta = 1 . 96 + 1 . 96 \sin\theta\]
\[\sin\theta = \frac{1}{2}\]
\[ \Rightarrow \theta = {30}^o\]
∴ Angle of projection = 90° − 30° = 60°
Time of reaching the ground,
\[\Rightarrow t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times (0 . 2 + 0 . 2\sin {30}^o )}{9 . 8}}\]
\[ \Rightarrow t = 0 . 247 s\]
Distance travelled in the horizontal direction is given by,
S = v cos θ × t
S = gr sin θ cos θ×t
S = 9.8 × 2 × 1232 × 0.247
S = 0.196 m
Total distance = (0.2 − 0.2 cos 30° + 0.196)
= 0.22 m
APPEARS IN
RELATED QUESTIONS
A bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays at rest with respect to the car with the string making an angle θ with the vertical. The linear momentum of the bob as seen from the road is increasing with time. Is it a violation of conservation of linear momentum? If not, where is the external force changes the linear momentum?
Two bodies make an elastic head-on collision on a smooth horizontal table kept in a car. Do you expect a change in the result if the car is accelerated in a horizontal road because of the non inertial character of the frame? Does the equation "Velocity of separation = Velocity of approach" remain valid in an accelerating car? Does the equation "final momentum = initial momentum" remain valid in the accelerating car?
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
A bullet hits a block kept at rest on a smooth horizontal surface and gets embedded into it. Which of the following does not change?
Internal forces can change
A shell is fired from a cannon with a velocity V at an angle θ with the horizontal direction. At the highest point in its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other piece immediately after the explosion is
A block moving in air breaks in two parts and the parts separate
(a) the total momentum must be conserved
(b) the total kinetic energy must be conserved
(c) the total momentum must change
(d) the total kinetic energy must change
A ball hits a floor and rebounds after an inelastic collision. In this case
(a) the momentum of the ball just after the collision is same as that just before the collision
(b) the mechanical energy of the ball remains the same during the collision
(c) the total momentum of the ball and the earth is conserved
(d) the total energy of the ball and the earth remains the same
A neutron initially at rest, decays into a proton, an electron, and an antineutrino. The ejected electron has a momentum of 1.4 × 10−26 kg-m/s and the antineutrino 6.4 × 10−27kg-m/s.
Find the recoil speed of the proton
(a) if the electron and the antineutrino are ejected along the same direction and
(b) if they are ejected along perpendicular directions. Mass of the proton = 1.67 × 10−27 kg.
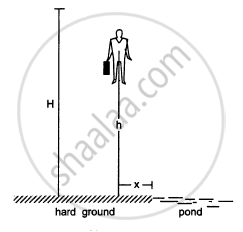
A man of mass M having a bag of mass m slips from the roof of a tall building of height H and starts falling vertically in the following figure. When at a height h from the ground, the notices that the ground below him is pretty hard, but there is a pond at a horizontal distance x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
Consider a head-on collision between two particles of masses m1 and m2. The initial speeds of the particles are u1 and u2 in the same direction. the collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle varies as \[v(t) = u_1 + \frac{t}{∆ t}( v_1 - u_1 )\]
Find the speed of the second particle as a function of time during the collision.
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
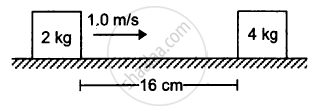
The friction coefficient between the horizontal surface and each of the block shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g = 10 m/s2.
Suppose the particle of the previous problem has a mass m and a speed \[\nu\] before the collision and it sticks to the rod after the collision. The rod has a mass M. (a) Find the velocity of the centre of mass C of the system constituting "the rod plus the particle". (b) Find the velocity of the particle with respect to C before the collision. (c) Find the velocity of the rod with respect to C before the collision. (d) Find the angular momentum of the particle and of the rod about the centre of mass C before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. (f) Find the velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

