Advertisements
Advertisements
Question
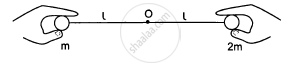
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
Solution
Given:
Mass of the 1st ball = m
Mass of the 2nd ball = 2m
When the balls reach the lower end,
Let the velocity of m be v; and the velocity of 2m be v'.
Using the work-energy theorem, we can write:
\[\left( \frac{1}{2} \right) \times m v^2 - \left( \frac{1}{2} \right) \times m(0 )^2 = mgl\]
\[ \Rightarrow v = \sqrt{2gl}\]
\[\text{ Similarly, velocity of block having mass 2m will be, }\]
\[v' = \sqrt{2gl}\]
\[\therefore v = v' = u (say)\]
Let the velocities of m and 2m after the collision be v1 and v2 respectively.
Using the law of conservation of momentum, we can write:
\[m \times u - 2mu = m v_1 + 2m v_2 \]
\[ \Rightarrow v_1 + 2 v_2 = - u . . . (1)\]
\[\text{ On applying collision formula, we get: }\]
\[ v_1 - v_2 = [(u - v)] = - 2u . . . (2)\]
\[\text{ Substracting equation } \left( 1 \right) \text{ from } \left( 2 \right), \text{ we get: } \]
\[3 v_2 = u\]
\[ \Rightarrow v_2 = \frac{u}{3} = \sqrt{\frac{2gl}{3}}\]
\[\text{ Substituting this value in equation (1), we get: }\]
\[ v_1 - v_2 = - 2u\]
\[ \Rightarrow v_1 = - 2u + v_2 \]
\[ = - 2u + \left( \frac{u}{3} \right)\]
\[ = \frac{- 5}{3}u = \frac{- 5}{3} \times \sqrt{2gl}\]
\[ = \frac{- \sqrt{50gl}}{3}\]
(b) Let the heights reached by balls 2m and m be h1 and h respectively.
Using the work energy principle, we get:
\[\left( \frac{1}{2} \right) \times 2m \times (0 )^2 - \left( \frac{1}{2} \right) \times 2m \times \left( v_2 \right)^2 = - 2m \times g \times h_1 \]
\[ \Rightarrow h_1 = \left( \frac{l}{9} \right)\]
\[\text{ Similarly,} \]
\[\left( \frac{1}{2} \right) \times m \times (0 )^2 - \left( \frac{1}{2} \right) \times m v_1^2 = m \times g \times h_2 \]
\[ \Rightarrow \left( \frac{1}{2} \right) \times \frac{50gl}{9} = g \times h_2 \]
\[ \Rightarrow h_2 = \frac{25l}{9}\]
As h2 is more than 2l, the velocity at the highest point will not be zero.
Also, the mass m will rise by a distance 2l.
APPEARS IN
RELATED QUESTIONS
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.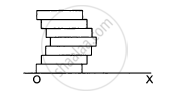
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.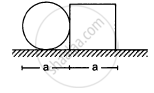
Calculate the velocity of the centre of mass of the system of particles shown in figure.

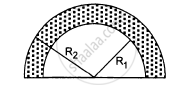
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
In an elastic collision
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
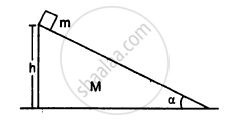
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
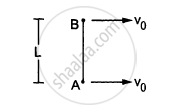
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
[Hint : The light rod will exert a force on the ball B
only along its length.]
The centre of mass of a system of particles does not depend upon, ______
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
The centre of mass of a system of two particles divides the distance between them ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
For which of the following does the centre of mass lie outside the body?
Which of the following points is the likely position of the centre of mass of the system shown in figure?
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
