Advertisements
Advertisements
प्रश्न
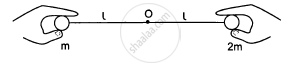
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
उत्तर
Given:
Mass of the 1st ball = m
Mass of the 2nd ball = 2m
When the balls reach the lower end,
Let the velocity of m be v; and the velocity of 2m be v'.
Using the work-energy theorem, we can write:
\[\left( \frac{1}{2} \right) \times m v^2 - \left( \frac{1}{2} \right) \times m(0 )^2 = mgl\]
\[ \Rightarrow v = \sqrt{2gl}\]
\[\text{ Similarly, velocity of block having mass 2m will be, }\]
\[v' = \sqrt{2gl}\]
\[\therefore v = v' = u (say)\]
Let the velocities of m and 2m after the collision be v1 and v2 respectively.
Using the law of conservation of momentum, we can write:
\[m \times u - 2mu = m v_1 + 2m v_2 \]
\[ \Rightarrow v_1 + 2 v_2 = - u . . . (1)\]
\[\text{ On applying collision formula, we get: }\]
\[ v_1 - v_2 = [(u - v)] = - 2u . . . (2)\]
\[\text{ Substracting equation } \left( 1 \right) \text{ from } \left( 2 \right), \text{ we get: } \]
\[3 v_2 = u\]
\[ \Rightarrow v_2 = \frac{u}{3} = \sqrt{\frac{2gl}{3}}\]
\[\text{ Substituting this value in equation (1), we get: }\]
\[ v_1 - v_2 = - 2u\]
\[ \Rightarrow v_1 = - 2u + v_2 \]
\[ = - 2u + \left( \frac{u}{3} \right)\]
\[ = \frac{- 5}{3}u = \frac{- 5}{3} \times \sqrt{2gl}\]
\[ = \frac{- \sqrt{50gl}}{3}\]
(b) Let the heights reached by balls 2m and m be h1 and h respectively.
Using the work energy principle, we get:
\[\left( \frac{1}{2} \right) \times 2m \times (0 )^2 - \left( \frac{1}{2} \right) \times 2m \times \left( v_2 \right)^2 = - 2m \times g \times h_1 \]
\[ \Rightarrow h_1 = \left( \frac{l}{9} \right)\]
\[\text{ Similarly,} \]
\[\left( \frac{1}{2} \right) \times m \times (0 )^2 - \left( \frac{1}{2} \right) \times m v_1^2 = m \times g \times h_2 \]
\[ \Rightarrow \left( \frac{1}{2} \right) \times \frac{50gl}{9} = g \times h_2 \]
\[ \Rightarrow h_2 = \frac{25l}{9}\]
As h2 is more than 2l, the velocity at the highest point will not be zero.
Also, the mass m will rise by a distance 2l.
APPEARS IN
संबंधित प्रश्न
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.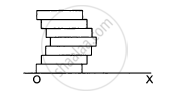
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.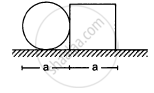
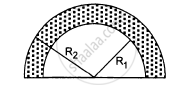
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Which of the following points is the likely position of the centre of mass of the system shown in figure?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.