Advertisements
Advertisements
प्रश्न
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

उत्तर
The mass of the bob is m.
The mass of the cart is M.
Considering the bob falls at point A.
Initial distance of centre of mass of the system from P is given as
\[x = \frac{m \times L + M \times 0}{M + m} = \frac{m}{M + m}L\]
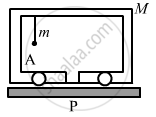
When the bob falls in the slot, the distance of centre of mass of the system from P becomes zero.
\[\therefore \text{ Shift in centre of mass } = 0 - \frac{mL}{M + m}\]
\[ = - \frac{mL}{M + m} \text{ towards left}\]
\[ = \frac{mL}{M + m} \text{ towards right}\]
Therefore, the cart moves a distance of
\[\frac{mL}{M + m}\] towards right.
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 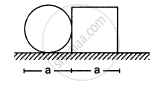
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
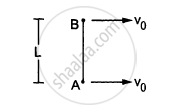
[Hint : The light rod will exert a force on the ball B
only along its length.]
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
The centre of mass of a system of particles does not depend upon, ______
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
Centre of mass is a point ______.
Which of the following points is the likely position of the centre of mass of the system shown in figure?