Advertisements
Advertisements
प्रश्न
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
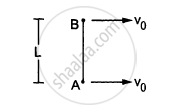
[Hint : The light rod will exert a force on the ball B
only along its length.]
उत्तर
(a) Collision will not affect the velocity of ball B because the light rod will exert a force on it only along its length.
Therefore, we have
Velocity of B = v0
For ball A,
On applying the law of conservation of linear momentum, we get
\[m \nu_0 = 2m \times \nu\]
\[\Rightarrow v = \frac{v_0}{2}\]
\[\therefore\] Velocity of A \[= \frac{\nu_0}{2}\]
(b) If we consider the three bodies to be a system, we have
Net external force = 0
\[v_{CM} = \frac{m \times v_0 + 2m \times \left( v_0 /2 \right)}{n + 2m}\]
\[ = \frac{m v_0 + m v_0}{3m}\]
\[ = \frac{2 v_0}{3}\]
(Direction will be same as the initial velocity before collision.)
(c) Velocity of (A + P) w.r.t. the centre of mass \[= \left\{ \frac{2 v_0}{3} - \frac{v_0}{2} \right\} = \frac{v_0}{6}\]
Velocity of B w.r.t. the centre of mass \[= v_0 - \frac{2 v_0}{3} = \frac{v_0}{3}\]
Distance of the (A + P) from the centre of mass \[= \frac{l}{3}\]
Distance of the B from the centre of mass = \[\frac{2l}{3}\]
Applying \[m v_{com} r = l_{cm} \times \omega, \] we have
\[\left( 2m \times \frac{v_o}{6} \times \frac{l}{3} \right) + \left( m \times \frac{v_0}{3} \times \frac{2l}{3} \right) = \left\{ 2m \left( \frac{l}{3} \right)^2 + \left( \frac{2l}{3} \right)^2 m \right\} \times \omega\]
\[ \Rightarrow \frac{6m v_0 l}{18} = \frac{6ml}{9}\omega\]
\[ \Rightarrow \omega = \frac{v_0}{2l}\]
APPEARS IN
संबंधित प्रश्न
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.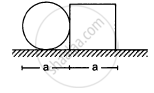
Calculate the velocity of the centre of mass of the system of particles shown in figure.

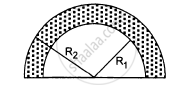
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
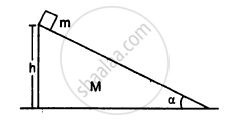
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
The centre of mass of a system of two particles divides the distance between them ______.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
Centre of mass is a point ______.
Which of the following points is the likely position of the centre of mass of the system shown in figure?