Advertisements
Advertisements
प्रश्न
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
उत्तर
Given:
The mass of the railroad car is M.
The mass of the man is m.
The car recoils with a speed v, backwards on the rails.
Let the man of mass m approaches towards the engine with a velocity v' w.r.t the engine.
∴ The velocity of man w.r.t earth is v' − v, towards right.
\[V_{centre of mass} = 0 (\text{Initially at rest })\]
\[ \therefore 0 = - Mv + m(v' - v)\]
\[ \Rightarrow Mv = m(v' - v)\]
\[ \Rightarrow mv' = Mv + mv\]
\[ \Rightarrow v' = \left( \frac{M + m}{m} \right)v\]
\[ \Rightarrow v' = \left( 1 + \frac{M}{m} \right)v\]
APPEARS IN
संबंधित प्रश्न
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 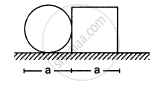
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.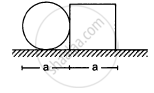
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Define centre of mass.
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
The centre of mass of a system of two particles divides the distance between them ______.
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
For which of the following does the centre of mass lie outside the body?
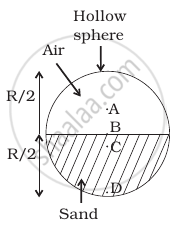
Which of the following points is the likely position of the centre of mass of the system shown in figure?
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
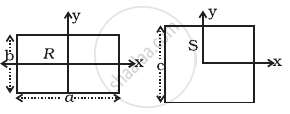
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
