Advertisements
Advertisements
प्रश्न
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.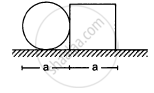
उत्तर
Let m be the mass per unit area of the square plate and the circular disc .
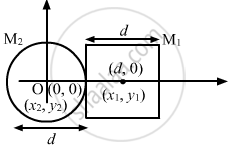
\[\Rightarrow\] Mass of the square plate, M1 = d2m
Mass of the circular disc, M2 = \[\frac{\pi d^2}{4}m\]
Let the centre of the circular disc be the origin of the system.
\[\Rightarrow\] x1 = d, y1 = 0
x2 = 0, y2 = 0
\[\Rightarrow\] Position of the centre of mass of circular disc and square plate:
\[= \left( \frac{m_1 x_1 + m_2 x_2}{m_1 + m_2}, \frac{m_1 y_1 + m_2 y_2}{m_1 + m_2} \right)\]
\[ = \left( \frac{d^2 md + \pi\left( d^2 /4 \right) m \times 0}{d^2 m + \pi \left( d^2 /4 \right) m}, \frac{0 + 0}{m_1 + m_2} \right)\]
\[ = \left( \frac{d^3 m}{d^2 m(1 + \pi/4)}, 0 \right)\]
\[ = \left( \frac{4d}{\pi + 4}, 0 \right)\]
Hence, the new centre of mass of the system (circular disc plus square plate) lies at distance \[\frac{4d}{(\pi + 4)}\] from the centre of circular disc, towards right.
APPEARS IN
संबंधित प्रश्न
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
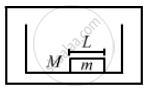
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
In an elastic collision
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
The centre of mass of a system of two particles divides the distance between them ______.
The radius and mass of earth are increased by 0.5%. Which of the following statements are true at the surface of the earth?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at ______.
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
