Advertisements
Advertisements
प्रश्न
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
उत्तर
It is given that:
Mass of Mr. Verma, m1 = 50 kg
Mass of Mr. Mathur, m2 = 60 kg
Mass of boat, m3 = 40 kg
Let A be the origin of the system (boat plus two men).
Initially, Mr. Verma and Mr. Mathur were at two extremes of the boat.
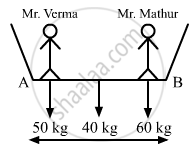
∴ Distance of the centre of mass:
\[X_{cm} = \frac{m_1 \times x_1 + m_2 \times x_2 + m_3 \times x_3}{m_1 + m_2 + m_3}\]
\[ = \frac{60 \times 0 + 50 \times 4 + 40 \times 2}{60 + 50 + 40}\]
\[ = \frac{280}{150} = 1 . 87 \text{ m from A}\]
As no external force is experienced in longitudinal direction, the centre of mass would not shift.
Initially, the centre of mass lies at a distance of 2 m from A.
When the men move towards the middle of the boat, the centre of mass shifts and lies at 1.87 m from A.
Therefore, the shift in centre of mass = 2 − 1.87 = 0.13 m, towards right
Hence, the boat moves 13 cm or 0.13 m towards right.
APPEARS IN
संबंधित प्रश्न
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
In an elastic collision
The centre of mass of a system of particles is at the origin. It follows that
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
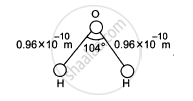
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Calculate the velocity of the centre of mass of the system of particles shown in figure.

A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
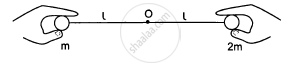
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
Solve the following problem.
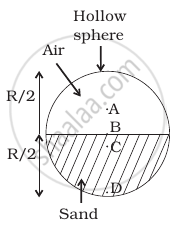
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of particles does not depend upon, ______
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
Centre of mass is a point ______.
Which of the following statements are correct?
Which of the following points is the likely position of the centre of mass of the system shown in figure?
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
