Advertisements
Advertisements
प्रश्न
Calculate the velocity of the centre of mass of the system of particles shown in figure.

उत्तर
From the figure, the velocities of different masses can be written as:
\[\text{For m}_1 = 1 . 0 \text{kg}, \]
\[\text{ Velocity, } \vec{v}_1 = \left( - 1 . 5 \cos 37^\circ \hat i - 1.5 \sin 37^\circ\hat j\right) = - 1 . 2 \hat i- 0.9 \hat j\]
\[\text{For m}_2 = 1 . 2 \text{kg}, \]
\[\text{Velocity}, \vec{v}_2 = 0 . 4 \vec{j} \]
\[\text{For m}_3 = 1 . 5 \text{kg,} \]
\[\text{Velocity,} \vec{v}_3 = - 1 . 0 \cos 37^\circ \hat i0 + 1.0 \sin 37^\circ\hat j \]
\[\text{ For m}_4 = 0 . 50 \text{kg}, \]
\[\text{ Velocity,} \vec{v}_4 = 3 . 0 \hat i \]
\[\text{ For m}_5 = 1 . 0 \text{ kg}, \]
\[\text{ Velocity }, \vec{v}_5 = 2 . 0 \cos 37^\circ \hat i - 2 . 0 \sin 37^\circ \hat j \]
\[(\cos 37^\circ = \frac{4}{5} \text{ and } \sin 37^\circ \ = \frac{3}{5})\]
\[ V_{cm} = \frac{m_1 \vec{v}_1 + m_2 \vec{v}_2 + m_3 \vec{v}_3 + m_4 \vec{v}_4 + m_5 \vec{v}_5}{m_1 + m_2 + m_3 + m_4 + m_5}\]
\[ = \frac{1}{1 . 0 + 1 . 2 + 1 . 5 + 1 . 0 + 0 . 50}^\left[ 1 . 0\left( - 1 . 5 \times \frac{4}{5} \vec{i} - 1 . 5 \times \frac{3}{5} \vec{j} \right) + . . . - 2 . 0 \times \frac{3}{5} \vec{j} \right] \]
On solving the above equation, we get:
Vcm is 0.20 m/s , at 45° below the direction, towards right.
APPEARS IN
संबंधित प्रश्न
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 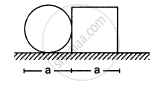
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
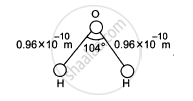
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
In an elastic collision
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
