Advertisements
Advertisements
प्रश्न
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
पर्याय
A implies B and B implies A.
A does not imply B and B does not imply A.
A implies B but B does not imply A.
B implies A but A does not imply B.
उत्तर
B implies A but A does not imply B.
The centre of mass of a system is given by,
\[\vec{R} = \frac{1}{M} \sum_{} m_i \vec{r}_i\]
On differentiating the above equation with respect to time, we get:
\[\frac{d \vec{R}}{dt} = \frac{1}{M} \sum_{} m_i \frac{d \vec{r}_i}{d t}\]
As the centre of mass of the system remains at rest, we have:
\[\frac{1}{M} \sum_{} m_i \frac{d \vec{r}_i}{d t} = 0\]
\[ \sum_{} m_i \vec{v}_i = 0\]
This implies that the linear momentum of the system remains constant.
APPEARS IN
संबंधित प्रश्न
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
In an elastic collision
The centre of mass of a system of particles is at the origin. It follows that
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
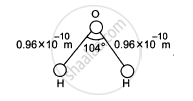
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
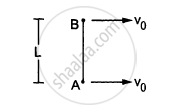
[Hint : The light rod will exert a force on the ball B
only along its length.]
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
For which of the following does the centre of mass lie outside the body?
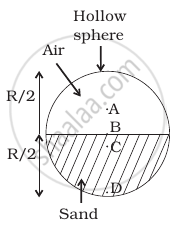
Which of the following points is the likely position of the centre of mass of the system shown in figure?
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at ______.
