Advertisements
Advertisements
प्रश्न
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
उत्तर
(a) Take a system of i moving particles.
Mass of the ith particle = mi
Velocity of the ith particle = vi
Hence, momentum of the ith particle, pi = mi vi
Velocity of the centre of mass = V
The velocity of the ith particle with respect to the centre of mass of the system is given as:
v’i = vi – V … (1)
Multiplying mi throughout equation (1), we get:
mi v’i = mi vi – mi V
p’i = pi – mi V
Where,
pi’ = mivi’ = Momentum of the ith particle with respect to the centre of mass of the system
∴pi = p’i + mi V
We have the relation: p’i = mivi’
Taking the summation of the momentum of all the particles with respect to the centre of mass of the system, we get:
`sum_("i") "p"_"t" = sum_("i")"m"
_"iv"_"t" = sum_("i")"m"_"i" ("dr"_"t")/"dt"`
Where
`"r""'"_"t" `= Position vector of the ith particle with respect to the centre of mass
`"v"_"t" = ("dr"_"t")/"dt"`
As per the definition of the centre of mass, we have
`sum_("i") "m"_"ir"_"t" = 0`
`:. sum_("i") "m"_"i" ("dr"_"t")/"dt" = 0`
`sum_("i") "p"_"i" = 0`
(b) We have the relation for the velocity of the ith particle as:
vi = v’i + V
`sum_("i")"m"_"i" "v"_"i" = sum_("i") "m"_"i" "v"_"t" + sum_("i")"m"_"i" "V"` ....(2)
Taking the dot product of equation (2) with itself, we get:
`sum_("i")"m"_"i" "v"_"i" .sum_("i") "m"_"iv"_"i" = sum_("i") "m"_"i"("v"_"i" + "V").sum_("i") "m"_"i"("v"_"i" + "V")`
`"M"^2sum_("i") "v"_"i"^2 = "M"^2 sum_("i") "v"_"i"^2 + "M"^2 sum_("i") "v"_"i". "v"_"i"+ "M"^2 sum_("i") "v"_"i"."v"_"i" + "M"^2"V"^2`
Here, for the centre of mass of the system of particle
`sum_("i")"v"_"i"."v"_"i" =-sum_("i")"v"_"i"."v"_"i"`
`"M"^2sum_("i") "v"_"i"^2 = "M"^2 sum_("i")"v"^2_"i" + "M"^2"V"^2`
`1/2 "M" sum_("i") "v"_"i"^('2) = 1/2 "M" sum_("i") "v"_"i"^('2) + 1.2 "MV"^2 `
`"K" = "K" + 1/2 "MV"^2`
Where
`"K" = 1/2 "M"sum_("i")"v"_"i"
^2` = Total kinetic energy of the system of particles
`"K""'" = 1/2 "M" sum_("i")"v"_"i"^(2)` = Total kinetic energy of the system of particles with respect to the centre of mass
`1/2 "MV"^2` = Kinetic energy of the translation of the system as a whole.
(c) Position vector of the ith particle with respect to origin = ri
Position vector of the ith particle with respect to the centre of mass = r’i
Position vector of the centre of mass with respect to the origin = R
It is given that:
r’i = ri – R
ri = r’i + R
We have from part (a),
pi = p’i + mi V
Taking the cross product of this relation by ri, we get:
`sum_("i")"r"_"i" xx "p"_"i" = sum_("i")"r"_"i"xx"p""'"_"i" + sum_("i") "r"_"i" xx "m"_"i" "V"`
`"L" = sum_("i") ("r""'"_"i" + "R" )xx "p""'"_"i" + sum_("i")("r""'"_"i" + "R") xx "m"_"iV"`
`= sum_("i")"r""'"_"i" xx "p""'"_"i" + sum_("i") ("r""'"_"i"+ "R") xx "m"_"iV"`
`= "L""'" + sum_("i") + sum_("i")"R" xx "p""'"_"i" + sum_("i") "r""'"_"i" xx "m"_"iV"+ sum_("i")"R" xx "m"_"iV"`
Where
`"R" xx sum_("i") "p""'"_"i" = 0` and `(sum_("i")"r""'"_"i") xx "MV" = 0`
`sum_("i") "m"_"i" = "M"`
`:."L" = "L""'" + "R" xx "MV"`
(d) Show `("dL""'")/"dt" = sum "r'"_"t" xx ("dp""'")/"dt"`
Further, show that
`("dL'")/("dt") = tau"'"_"ext"`
where `tau"'"_"ext"` is the sum of all external torques acting on the system about the
centre of mass.
(Hint : Use the definition of centre of mass and Newton’s Third Law. Assume the internal forces between any two particles act along the line joining the particles.)
APPEARS IN
संबंधित प्रश्न
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 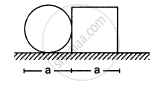
The centre of mass of a system of particles is at the origin. It follows that
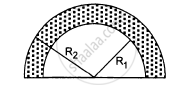
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
The centre of mass of a system of particles does not depend upon, ______
