Advertisements
Advertisements
प्रश्न
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
उत्तर
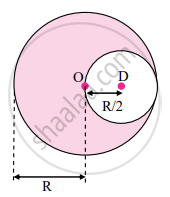
Let the centre of the sphere be origin O. Then, r1 be the position vector of the centre of mass of uniform solid sphere and r2 be the position vector of the centre of mass of the cut-out part of the sphere.
Now, mass of the sphere is given as,
M = `(4/3 pi"R"^3)rho` ....(i)
Hence, the mass of the cut part of the sphere will be,
M' = `[4/3 pi("R"/2)^3]rho` .....(∵ sphere is uniform, ρ = constant)
∴ M' = `(4/3 pi"R"^3)rho xx 1/8`
`= "M"/8` ....[From (i)]
From figure, r1 = 0, r2 = `"R"/2`
∴ Position vector of centre of mass of remaining part,
`"r"_"cm" = ("M" xx "r"_1 - "M'" xx "r"_2)/("M" - "M'")`
`= ("M" xx 0 - ("M"/8) xx "R"/2)/("M" - "M"/8)`
`= ((- "RM")/16 xx 8/"7M")`
`"r"_"cm" = (-"R")/14`
(Negative sign indicates the distance is on left side of the origin.)
Position of centre of mass of remaining sphere is `(-"R")/14`
APPEARS IN
संबंधित प्रश्न
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 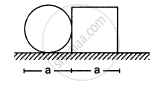
The centre of mass of a system of particles is at the origin. It follows that
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
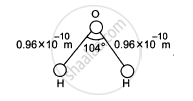
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
In an elastic collision
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
Define centre of mass.
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
The radius and mass of earth are increased by 0.5%. Which of the following statements are true at the surface of the earth?
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Which of the following points is the likely position of the centre of mass of the system shown in figure?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
