Advertisements
Advertisements
प्रश्न
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
उत्तर
(a) Yes
Consider a charge distributed in X-Y plane.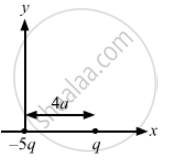
\[X_{cm} = \frac{- 6q \times 0 + q \times 5a}{- 6q + q} = - a\]
(b) Yes. Because the z-coordinates of all the charges are zero, the centre of charge lies in X-Y plane.
(c) No, it is not necessary that the centre of charge lies in the cube because charge can be either negative or positive.
APPEARS IN
संबंधित प्रश्न
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
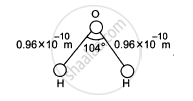
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Calculate the velocity of the centre of mass of the system of particles shown in figure.

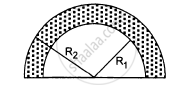
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
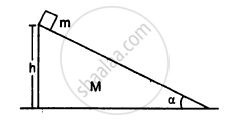
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
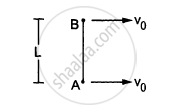
[Hint : The light rod will exert a force on the ball B
only along its length.]
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
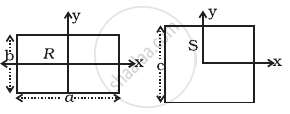
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
