Advertisements
Advertisements
Question
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
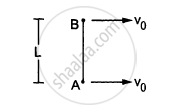
[Hint : The light rod will exert a force on the ball B
only along its length.]
Solution
(a) Collision will not affect the velocity of ball B because the light rod will exert a force on it only along its length.
Therefore, we have
Velocity of B = v0
For ball A,
On applying the law of conservation of linear momentum, we get
\[m \nu_0 = 2m \times \nu\]
\[\Rightarrow v = \frac{v_0}{2}\]
\[\therefore\] Velocity of A \[= \frac{\nu_0}{2}\]
(b) If we consider the three bodies to be a system, we have
Net external force = 0
\[v_{CM} = \frac{m \times v_0 + 2m \times \left( v_0 /2 \right)}{n + 2m}\]
\[ = \frac{m v_0 + m v_0}{3m}\]
\[ = \frac{2 v_0}{3}\]
(Direction will be same as the initial velocity before collision.)
(c) Velocity of (A + P) w.r.t. the centre of mass \[= \left\{ \frac{2 v_0}{3} - \frac{v_0}{2} \right\} = \frac{v_0}{6}\]
Velocity of B w.r.t. the centre of mass \[= v_0 - \frac{2 v_0}{3} = \frac{v_0}{3}\]
Distance of the (A + P) from the centre of mass \[= \frac{l}{3}\]
Distance of the B from the centre of mass = \[\frac{2l}{3}\]
Applying \[m v_{com} r = l_{cm} \times \omega, \] we have
\[\left( 2m \times \frac{v_o}{6} \times \frac{l}{3} \right) + \left( m \times \frac{v_0}{3} \times \frac{2l}{3} \right) = \left\{ 2m \left( \frac{l}{3} \right)^2 + \left( \frac{2l}{3} \right)^2 m \right\} \times \omega\]
\[ \Rightarrow \frac{6m v_0 l}{18} = \frac{6ml}{9}\omega\]
\[ \Rightarrow \omega = \frac{v_0}{2l}\]
APPEARS IN
RELATED QUESTIONS
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
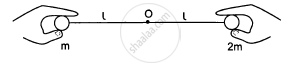
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
Define centre of mass.
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
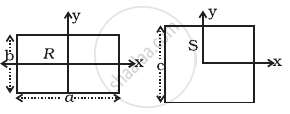
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
