Advertisements
Advertisements
Question
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
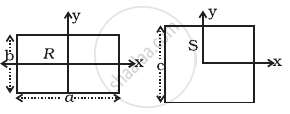
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
Solution
According to the problem,
Area of square = area of rectangular plate
⇒ `c^2 = a xx b`
⇒ `c^2 = ab`
a. `I_(xR)/I_(xS) = b^2/c^2` ......[∵ I ∝ (area)2]
It is clear from the diagram that b < c
⇒ `I_(xR)/I_(xS) = (b/c)^2 < 1`
⇒ `I_(xR) < I_(xS)`
b. `I_(yR)/I_(yS) = a^2/c^2` ......(It is clear that a < c)
`I_(yR)/I_(yS) - (a/c)^2 > 1`
c. `I_(zR) = 1/12 M(a^2 + b^2)`
`I_(zS) = 1/12 M(c^2 + c^2)`
Now, `I_(zR) - I_(zS) = 1/12 M[a^2 + b^2 - 2c^2]`
= `1/12 M(a^2 + b^2 - 2ab)`
`I_(zR) - I_(zS) = 1/12 M(a - b)^2 > 0`
⇒ `I_(zR)/I_(zS) > 1`
APPEARS IN
RELATED QUESTIONS
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Calculate the velocity of the centre of mass of the system of particles shown in figure.

A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
In an elastic collision
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Which of the following points is the likely position of the centre of mass of the system shown in figure?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
