Advertisements
Advertisements
प्रश्न
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
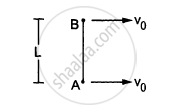
[Hint : The light rod will exert a force on the ball B
only along its length.]
उत्तर
(a) Collision will not affect the velocity of ball B because the light rod will exert a force on it only along its length.
Therefore, we have
Velocity of B = v0
For ball A,
On applying the law of conservation of linear momentum, we get
\[m \nu_0 = 2m \times \nu\]
\[\Rightarrow v = \frac{v_0}{2}\]
\[\therefore\] Velocity of A \[= \frac{\nu_0}{2}\]
(b) If we consider the three bodies to be a system, we have
Net external force = 0
\[v_{CM} = \frac{m \times v_0 + 2m \times \left( v_0 /2 \right)}{n + 2m}\]
\[ = \frac{m v_0 + m v_0}{3m}\]
\[ = \frac{2 v_0}{3}\]
(Direction will be same as the initial velocity before collision.)
(c) Velocity of (A + P) w.r.t. the centre of mass \[= \left\{ \frac{2 v_0}{3} - \frac{v_0}{2} \right\} = \frac{v_0}{6}\]
Velocity of B w.r.t. the centre of mass \[= v_0 - \frac{2 v_0}{3} = \frac{v_0}{3}\]
Distance of the (A + P) from the centre of mass \[= \frac{l}{3}\]
Distance of the B from the centre of mass = \[\frac{2l}{3}\]
Applying \[m v_{com} r = l_{cm} \times \omega, \] we have
\[\left( 2m \times \frac{v_o}{6} \times \frac{l}{3} \right) + \left( m \times \frac{v_0}{3} \times \frac{2l}{3} \right) = \left\{ 2m \left( \frac{l}{3} \right)^2 + \left( \frac{2l}{3} \right)^2 m \right\} \times \omega\]
\[ \Rightarrow \frac{6m v_0 l}{18} = \frac{6ml}{9}\omega\]
\[ \Rightarrow \omega = \frac{v_0}{2l}\]
APPEARS IN
संबंधित प्रश्न
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
In an elastic collision
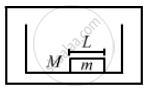
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
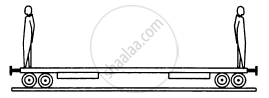
Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
Define centre of mass.
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
The centre of mass of a system of two particles divides the distance between them ______.
The radius and mass of earth are increased by 0.5%. Which of the following statements are true at the surface of the earth?
For which of the following does the centre of mass lie outside the body?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
