Advertisements
Advertisements
प्रश्न
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
उत्तर
Let the masses of the two particles be m1 and m2.
Given:
m1 = 1 kg
m2 = 4 kg
Now,
Kinetic energy of the first particle = Kinetic energy of the second particle
\[\left( \frac{1}{2} \right) m_1 v_1^2 = \left( \frac{1}{2} \right) m_2 v_2^2 \]
\[ \Rightarrow \frac{m_1}{m_2} = \frac{v_2^2}{v_1^2}\]
\[ \Rightarrow \frac{v_2}{v_1} = \sqrt{\frac{m_1}{m_2}}\]
\[ \Rightarrow \frac{v_1}{v_2} = \sqrt{\frac{m_2}{m_1}}\]
\[\text{ The ratio of linear momenta (mv) of the two particles,} \]
\[\frac{P_1}{P_2} = \frac{m_1 v_1}{m_2 v_2} = \frac{m_1}{m_2}\sqrt{\frac{m_2}{m_1}}\]
\[ = \sqrt{\frac{m_1}{m_2}} = \sqrt{\frac{1}{4}} = \frac{1}{2}\]
\[ \Rightarrow P_1 : P_2 = 1: 2\]
Therefore, the ratio of linear momenta is 1:2.
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
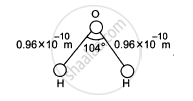
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.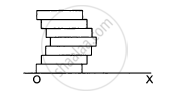
Calculate the velocity of the centre of mass of the system of particles shown in figure.

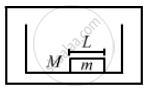
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
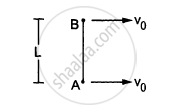
[Hint : The light rod will exert a force on the ball B
only along its length.]
Define centre of mass.
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
Which of the following has maximum momentum?
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
For which of the following does the centre of mass lie outside the body?
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
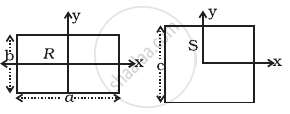
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
