Advertisements
Advertisements
Question
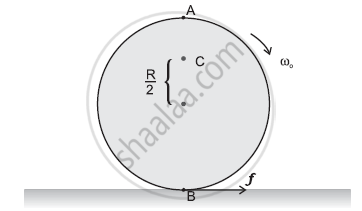
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
Solution 1
A torque is required to roll the given disc. As per the definition of torque, the rotating force should be tangential to the disc. Since the frictional force at point B is along the tangential force at point A, a frictional force is required for making the disc roll.
(a) Force of friction acts opposite to the direction of velocity at point B. The direction of linear velocity at point B is tangentially leftward. Hence, frictional force will act tangentially rightward. The sense of frictional torque before the start of perfect rolling is perpendicular to the plane of the disc in the outward direction.
(b) Since frictional force acts opposite to the direction of velocity at point B, perfect rolling will begin when the velocity at that point becomes equal to zero. This will make the frictional force acting on the disc zero.
Solution 2
To roll a disc, we require a torque, which can be provided only by a tangential force. As a force of friction is the only tangential force, in this case, it is necessary.
a)As frictional force at B opposes the velocity of point B, which is to the left, the frictional force must be to the right. The sense of frictional torque will be perpendicular to the plane of the disc and outwards.
(b)As frictional force at B decreases the velocity of the point of contact B with the surface, the perfect rolling begins only when a velocity of point B becomes zero. Also, force of friction would become zero at this stage.
APPEARS IN
RELATED QUESTIONS
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
A rod of mass 'm' hinged at one end is free to rotate in a horizontal plane. A small bullet of mass m/4 travelling with speed 'u' hits the rod and attaches to it at its centre. Find the angular speed of rotation of rod just after the bullet hits the rod 3. [take length of the rod as 'l']
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms-1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
The magnitude of the torque on a particle of mass 1 kg is 2.5 Nm about the origin. If the force acting on it is 1 N, and the distance of the particle from the origin is 5 m, the angle between the force and the position vector is (in radians) ______.
