Advertisements
Advertisements
प्रश्न
A galvanometer shows full-scale deflection for current Ig. A resistance R1 is required to convert it into a voltmeter of range (0 - V) and a resistance R2 to convert it into a voltmeter of range (0 - 2V). Find the resistance of the galvanometer.
Advertisements
उत्तर
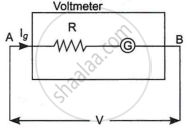
In the first case the potential difference between A and B,
`V = I_gR_1 + I_gG`
`I_g = V/(R_1 + G)`
Where G = Resistance of galvanometer
∴ `R_1 + G = V/I_g`
`R_1 = V/(Ig) - G`
⇒ G = `V/(Ig) - R_1`
In the second case,
`I_g = V/(R_2 + G)`
R2 is the Resistance required to change the range from 0 - 2V.
`I_g = (2V)/(R_2 + G)`
`R_2 + G = (2V)/I_g`
`R_2 = (2V)/I_g - G`
⇒ R = `(2V)/I_g - R_2`
Hence, the resistance of the galvanometer is respectively `V/(Ig) - R_1` and `(2V)/(Ig) - R_2`.
APPEARS IN
संबंधित प्रश्न
A rectangular coil of a moving coil galvanometer contains 50 turns each having area 12 cm2 . It is suspended in radial magnetic field 0.025 Wb/m2 by a fibre of twist constant 15 x10-10 Nm/degree. Calculate the sensitivity of the moving coil galvanometer.
An ideal voltmeter has _______.
(A) low resistance
(b) high resistance
(C) infinite resistance
(D) zero resistance
A galvanometer has a resistance of 16Ω. It shows full scale deflection, when a current of 20 mA is passed through it. The only shunt resistance available is 0.06 which is not appropriate to convert a galvanometer into an ammeter. How much resistance should be connected in series with the coil of galvanometer, so that the range of ammeter is 8 A?
State the underlying principle of working of a moving coil galvanometer. Write two reasons why a galvanometer can not be used as such to measure current in a given circuit. Name any two factors on which the current sensitivity of a galvanometer depends.
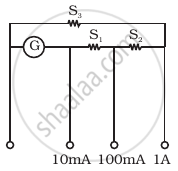
A multirange voltmeter can be constructed by using a galvanometer circuit as shown in figure. We want to construct a voltmeter that can measure 2V, 20V and 200V using a galvanometer of resistance 10Ω and that produces maximum deflection for current of 1 mA. Find R1, R2 and R3 that have to be used.
A galvanometer having a resistance of 20 Ω and 30 Ω division on both sides has figure of merit 0.005 ampere/division. The resistance that should be connected in series such that it can be used as a voltmeter upto 15 volt, is ______.
A resistance of 3Ω is connected in parallel to a galvanometer of resistance 297Ω. Find the fraction of current passing through the galvanometer.
A voltmeter has a range of 0 - 20 V and a resistance of 500 Q. Explain how can be used to measure voltages from 0 - 200 volt?
Assertion: When an electric current is passed through a moving coil galvanometer, its coil gets deflected.
Reason: A circular coil produces a uniform magnetic field around itself when an electric current is passed through it.
The figure below shows a circuit containing an ammeter A, a galvanometer G and a plug key K. When the key is closed:
