Advertisements
Advertisements
प्रश्न
A group of 1536 cadets wanted to have a parade forming a square design. Is it possible? If it is not possible, how many more cadets would be required?
उत्तर
Number of cadets to form square design
1536 = `bar(2 xx 2) xx bar(2 xx 2) xx bar(2 xx 2) xx bar(2 xx 2) xx 2 xx 3`
| 2 | 1536 |
| 2 | 768 |
| 2 | 384 |
| 2 | 192 |
| 2 | 96 |
| 2 | 48 |
| 2 | 24 |
| 2 | 12 |
| 2 | 6 |
| 3 |
The numbers 2 and 3 are unpaired
∴ It is impossible to have the parade forming square design with 1536 cadets.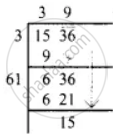
39 × 39 = 1521
Also 40 × 40 = 1600
∴ We have to add (1600 – 1536) = 64 to make 1536 a perfect square.
∴ 64 more cadets would be required to form the square design.
APPEARS IN
संबंधित प्रश्न
What will be the unit digit of the square of the given number?
799
The following number are obviously not perfect square. Give reason.
222222
The following number are obviously not perfect square. Give reason.
222000
The square of which of the following number would be an odd number?
731
Find the value of:
\[\frac{\sqrt{1587}}{\sqrt{1728}}\]
Evaluate: 1012 – 1002
The square of 75 is 4925
Find the length of a room whose area is `153/10` sq.m and whose breadth is `2 11/20` m
There is no square number between 50 and 60.
There are 200 natural numbers between 1002 and 1012.
