Question

A group of 1536 cadets wanted to have a parade forming a square design. Is it possible? If it is not possible, how many more cadets would be required?

Answer 1

Number of cadets to form square design

1536 = `bar(2 xx 2) xx bar(2 xx 2) xx bar(2 xx 2) xx bar(2 xx 2) xx 2 xx 3`

2	1536
2	768
2	384
2	192
2	96
2	48
2	24
2	12
2	6
	3

The numbers 2 and 3 are unpaired

∴ It is impossible to have the parade forming square design with 1536 cadets.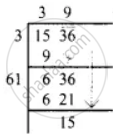

39 × 39 = 1521

Also 40 × 40 = 1600

∴ We have to add (1600 – 1536) = 64 to make 1536 a perfect square.

∴ 64 more cadets would be required to form the square design.