Advertisements
Advertisements
प्रश्न
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
उत्तर
Given, radius of hemispherical bowl, r = 9 cm
And radius of cylindrical bottles, R = 1.5 cm and height, h = 4 cm
∴ Number of required cylindrical bottles
= `"Volume of hemispherical bowl"/"Volume of one cylindrical bottle"`
= `(2/3 pir^3)/(pi R^2h)`
= `(2/3 xx pi xx 9 xx 9 xx 9)/(pi xx 1.5 xx 1.5 xx 4)`
= 54
APPEARS IN
संबंधित प्रश्न
500 persons have to dip in a rectangular tank which is 80m long and 50m broad. What is the rise in the level of water in the tank, if the average displacement of water by a person is 0.04m3 .
The diameters of internal and external surfaces of hollow spherical shell are 10cm and 6cm respectively. If it is melted and recast into a solid cylinder of length of 2`2/3`cm, find the
diameter of the cylinder.
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm, containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
A metal cube of side 11 cm is completely submerged in water contained in a cylindrical vessel with diameter 28 cm. Find the rise in the level of water.
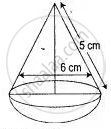
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
If the radius of base of a right circular cylinder is halved, keeping the height same, the ratio of the volume of the reduced cylinder to that of the original cylinder is ______.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
An ice-cream filled cone having radius 5 cm and height 10 cm is as shown in the figure. Find the volume of the ice-cream in 7 such cones.

