Question

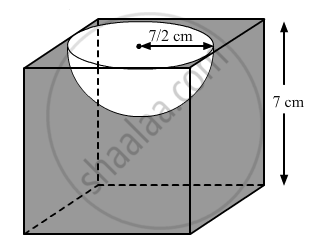
A hemispherical depression is cut out from one face of a cubical block of side 7 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid. [Use π = \[\frac{22}{7}\]]

Answer 1

For the cubical block:

Edge of the cube, a = 7 cm
For the hemisphere:
Diameter of the hemisphere = Length of a side of the cube = 7 cm

∴ Radius(r) of the hemisphere =\[\frac{7}{2} cm\]

Surface area of the remaining solid = Surface area of the cube − Surface area of the circle on one of the faces of the cube + Surface area of the hemisphere 

=\[6 a^2 - \pi r^2 + 2\pi r^2\]

=\[6 a^2 + \pi r^2\]

=\[\left( 6 \times 7^2 + \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \right) {cm}^2\]

=\[\left( 294 + 38 . 5 \right) {cm}^2\]

=\[332 . 5 {cm}^2\]

Thus, surface area of the remaining solid is 332.5 cm².