Advertisements
Advertisements
प्रश्न
A hydrogen atom initially in the ground level absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of the photon.
A hydrogen atom initially in the ground state absorbs a photon which excites it to the n = 4 level. Estimate the frequency of the photon
उत्तर
For ground level, n1 = 1
Let E1 be the energy of this level. It is known that E1 is related with n1 as:
`"E"_1 = (-13.6)/("n"_1^2) "eV"`
`= (-13.6)/1^2`
= −13.6 eV
The atom is excited to a higher level, n2 = 4.
Let E2 be the energy of this level.
∴ `"E"_2 = (-13.6)/"n"_2^2 "eV"`
= `(-13.6)/4^2`
= `(-13.6)/16 "eV"`
The amount of energy absorbed by the photon is given as:
E = E2 − E1
= `(-13.6)/16 - ((-13.6)/1)`
= `(13.6 xx 15)/16 "eV"`
= `(13.6 xx 15)/16 xx 1.6 xx 10^(-19)`
= 2.04 × 10−18 J
For a photon of wavelength λ, the expression of energy is written as:
`"E" = "hc"/lambda`
Where,
h = Planck’s constant = 6.6 × 10−34 Js
c = Speed of light = 3 × 108 m/s
∴ λ = `"hc"/"E"`
= `(6.6 xx 10^-34 xx 3 xx 10^8)/(2.04 xx 10^-18)`
= 9.7 × 10−8 m
= 97 nm
And, frequency of a photon is given by the relation,
`"v" = "c"/lambda`
= `(3 xx 10^8)/(9.7 xx 10^(-8))`
≈ 3.1 × 1015 Hz
Hence, the wavelength of the photon is 97 nm while the frequency is 3.1 × 1015 Hz.
APPEARS IN
संबंधित प्रश्न
Given the ground state energy E0 = - 13.6 eV and Bohr radius a0 = 0.53 Å. Find out how the de Broglie wavelength associated with the electron orbiting in the ground state would change when it jumps into the first excited state.
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited? Calculate the wavelengths of the first member of Lyman and first member of Balmer series.
The ground state energy of hydrogen atom is −13.6 eV. What are the kinetic and potential energies of the electron in this state?
The total energy of an electron in the first excited state of the hydrogen atom is about −3.4 eV.
What is the kinetic energy of the electron in this state?
Obtain the first Bohr’s radius and the ground state energy of a muonic hydrogen atom [i.e., an atom in which a negatively charged muon (μ−) of mass about 207 me orbits around a proton].
What are means by pair annihilation? Write a balanced equation for the same.
Wavelengths of the first lines of the Lyman series, Paschen series and Balmer series, in hydrogen spectrum are denoted by `lambda_L, lambda_P and lambda_B` respectively. Arrange these wavelengths in increasing order.
A 12.3 eV electron beam is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited?
Calculate the wavelengths of the second member of Lyman series and second member of Balmer series.
Draw the energy level diagram showing how the line spectra corresponding to Paschen series occur due to transition between energy levels.
The energy levels of an atom are as shown below. Which of them will result in the transition of a photon of wavelength 275 nm?

Which transition corresponds to emission of radiation of maximum wavelength?
A Carnot engine absorbs 1000 J of heat energy from a reservoir at 127°C and rejects 600 J of heat energy during each cycle. The efficiency of the engine and temperature of the sink will be:
The Ionisation energy of hydrogen atom is 3.6 ev The ionisation energy of helium atom would be
Energy of an electron at infinity from nucleus is ______.
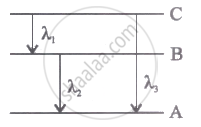
Energy levels A, B, C of acertain atom corresponding to increasing value of energy, i.e., EA< E8 < Ee. If λ1, λ2 and λ3 are the wavelength of radiations corresponding to the transitions C to B, B to A and C to A respectively, which of the following statements is correct?
Radiation coming from transitions n = 2 to n = 1 of hydrogen atoms fall on He+ ions in n = 1 and n = 2 states. The possible transition of helium ions as they absorb energy from the radiation is ______.
Which of the following is true for X-rays?
The diagram shows the four energy levels of an electron in the Bohr model of the hydrogen atom. Identify the transition in which the emitted photon will have the highest energy.