Advertisements
Advertisements
प्रश्न
A pharmaceutical company has four branches, one ea.ch at city A, B, C, D. A branch manager is to be appointed one at each city, out of four candidates P, Q, R and S. The monthly business deyending upon the city and the effectiveness of the branch manager in that city is given below :
| City | ||||
| A | B | C | D | |
| Monthly business (₹ lakh) | ||||
| P | 10 | 10 | 8 | 8 |
| Q | 12 | 15 | 10 | 9 |
| R | 11 | 16 | 12 | 7 |
| S | 15 | 13 | 15 | 11 |
Which manager should be appointed at which city so as to get the maximum total monthly business·?
उत्तर
Since it is a maximization problem . Subtract each of the elements in the table from the largest element.

Minimum element of each row is subtracted from every element in that row
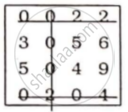
Minimum element of each column is subtracted from every element in that column.
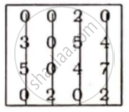
Since nwnber of lines covering all zeros is less than number of rows I columns.
∴ Subtract smallest uncovered element.

∴ Number of lines covering all zeros equal to number rows I column
∴ optimal solution has reached
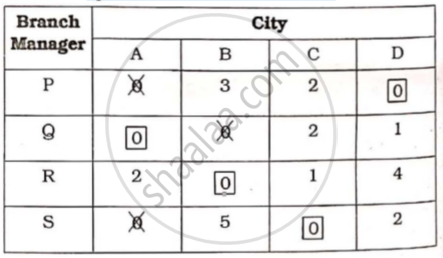
Optimum allocation is as follows.
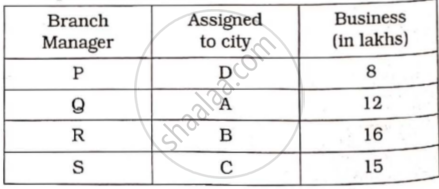
with total maximum business
8 + 12 + 16 + 15 = 51 (lakhs)
Assignment
P → D Q → A R → B S → C
APPEARS IN
संबंधित प्रश्न
Find the values of x and y, if
`2[[1,3],[0,x]]+[[y,0],[1,2]]=[[5,6],[1,8]]`
If `"A"=[[2,1],[1,1]] " then show taht " A^2-3A+I=0`
Find the values of x and y, if `2[(1, 3), (0, x)] + [(y, 0), (1, 2)] = [(5, 6), (1, 8)]`
Find the sequence that minimizes the total elapsed time (in hours) required to
complete the following jobs on the machine M1 , M2 and M3 in the order M1M2M3 :
| Machine Jobs | A | B | C | D |
| M1 | 5 | 6 | 9 | 5 |
| M2 | 2 | 4 | 5 | 3 |
| M3 | 3 | 5 | 6 | 7 |
Find x and y, if
`{ 3[(1, 2, 0), (0, -1, 3)] - [(1, 5, -2), (-3, -4, 4)]}[(1), (2), (1)] = [(x), (y)]`
Evaluate : `int tan^-1x dx`
Express the following equations in matrix form and solve them by the method of inversion.
x + 2y + 3z = 8,
2x - y + z = 1,
3x + y - 4z = 1
