Advertisements
Advertisements
प्रश्न
A pipe can fill a cistern in 10 hours. Due to a leak in the bottom it is filled in 12 hours. When the cistern is full, in how much time will it be emptied by the leak?
उत्तर
\[\text{ When there is no leakage, the pipe can fill the cistern in 10 hours } . \]
\[\text{ Thus, the pipe can fill } \frac{1}{10}\text{ th part of the cistern in 1 hour .} \]
\[\text{ When there is leakage, the pipe can fill the cistern in 12 hours } . \]
\[\text{ Therefore, in case of leakage, the pipe can fill } \frac{1}{12}\text{ th part of the cistern in 1 hour } . \]
\[\text{ Thus, in one hour, due to leakge, } \left( \frac{1}{10} - \frac{1}{12} \right)\text{ th or } \frac{1}{60}\text{ th part of the cistern is emptied } . \]
\[\text{ Hence, the cistern will be emptied by the leakage in 60 hours } .\]
APPEARS IN
संबंधित प्रश्न
Which of the following quantities vary directly with each other?
(i) Number of articles (x) and their price (y).
(ii) Weight of articles (x) and their cost (y).
(iii) Distance x and time y, speed remaining the same.
(iv) Wages (y) and number of hours (x) of work.
(v) Speed (x) and time (y) (distance covered remaining the same).
(vi) Area of a land (x) and its cost (y).
68 boxes of a certain commodity require a shelf-length of 13.6 m. How many boxes of the same commodity would occupy a shelf length of 20.4 m?
A and B can finish a work in 20 days. A alone can do \[\frac{1}{5}\] th of the work in 12 days. In how many days can B alone do it?
8 men can do a piece of work in 9 days. In how many days will 6 men do it?
If x = 5y, then x and y vary ______ with each other.
The perimeter of a circle and its diameter vary ______ with each other.
l varies directly as m and l is equal to 5, when `m = 2/3`. Find l when `m = 16/3`.
From the following table, determine if x and y are in direct proportion or not.
| x | 4 | 7 | 10 | 16 |
| y | 24 | 42 | 60 | 96 |
44 cows can graze a field in 9 days. How many less/more cows will graze the same field in 12 days?
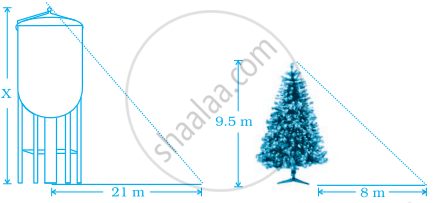
A water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proportional to their heights. Find the height of the tank.