Advertisements
Advertisements
प्रश्न
A point object is placed on the principal axis of a convex spherical surface of radius of curvature R, which separates the two media of refractive indices n1 and n2 (n2 > n1). Draw the ray diagram and deduce the relation between the object distance (u), image distance (v) and the radius of curvature (R) for refraction to take place at the convex spherical surface from rarer to denser medium.
Advertisements
उत्तर
A refracting surface which forms a part of a sphere of transparent refracting material is called a spherical refracting surface.
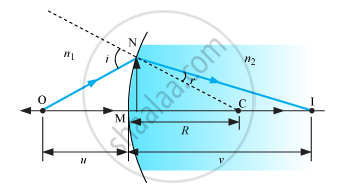
The above figure shows the geometry of formation of image I of an object O and the principal axis of a spherical surface with centre of curvature Cand radius of curvature R.
Assumptions:
(i) The aperture of the surface is small compared to other distance involved.
(ii) NM will be taken to be nearly equal to the length of the perpendicular from the point N on the principal axis.
`tan ∠NOM = (MN)/(OM)`
`tan ∠NCM =(MN)/(MC) `
`tan ∠NIM = (MN)/(MI)`
For ΔNOC, i is the exterior angle.
∴ i = ∠NOM + ∠NCM
`i = (MN)/(OM)+(MN)/(MC) ........... (1)`
Similarly, r = ∠NCM − ∠NIM
`i.e.,r = (MN)/(MC) - (MN)/(MI) ......(2) `
By Snell’s law,
n1sini = n2sinr
For small angles,
n1i= n2 r
Substituting the values of i and r from equations (i) and (ii), we obtain
`n_1( (MN)/(OM)+(MN)/(MC))= n_2((MN)/(MC) - (MN)/(MI)) `
or,`n_1/(OM) +n_2/(MI)= (n_2 - n_1)/(MC) ........... (3)`
Applying new Cartesian sign conventions,
OM = − u, MI = + v, MC = + R
Substituting these in equation (3), we obtain
`n_2/v-n_1/u = (n_2-n_1)/R ...... (4)`
Above equation is the required equation.
APPEARS IN
संबंधित प्रश्न
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 × 10−22 C/m2. What is E:
- in the outer region of the first plate,
- in the outer region of the second plate, and
- between the plates?
Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1 and C2 with their capacitances in the ratio 1 : 2 so that the energy stored in the two cases becomes the same.
A small conducting sphere of radius 'r' carrying a charge +q is surrounded by a large concentric conducting shell of radius Ron which a charge +Q is placed. Using Gauss's law, derive the expressions for the electric field at a point 'x'
(i) between the sphere and the shell (r < x < R),
(ii) outside the spherical shell.
Using Gauss’ law deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point
(i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R.
(r being the distance from the centre of the shell)
A rubber balloon is given a charge Q distributed uniformly over its surface. Is the field inside the balloon zero everywhere if the balloon does not have a spherical surface?
Find the flux of the electric field through a spherical surface of radius R due to a charge of 10−7 C at the centre and another equal charge at a point 2R away from the centre in the following figure.
A spherical volume contains a uniformly distributed charge of density 2.0 × 10 -4 Cm-3 Find the electric field at a point inside the volume at a distance 4⋅0 cm from the centre.
A circular wire-loop of radius a carries a total charge Q distributed uniformly over its length. A small length dL of the wire is cut off. Find the electric field at the centre due to the remaining wire.
“A uniformly charged conducting spherical shell for the points outside the shell behaves as if the entire charge of the shell is concentrated at its centre”. Show this with the help of a proper diagram and verify this statement.
