Advertisements
Advertisements
प्रश्न
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and it passes through the point (5, 3). Find the co-ordinates of the point A
उत्तर
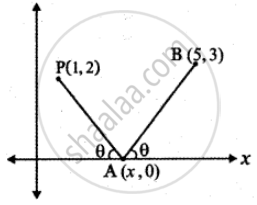
Let P(1, 2) and (5, 3) are the given points.
By the property of reflection,
∠XAB = ∠OAP = θ
(Angle of incidence = Angle of reflection)
Slope of the line OA(x – axis) m1 = 0
Slope of the line joining the points P(1, 2) and A(x, 0)
Slope of AP, m2 = `(2 - 0)/(1 - x) = 2/(1 - x)`
Slope of the line joining the points B(5, 3 ) and A(x, 0)
tan θ = `|("m"_1 + "m"_3)/(1 + "m"_1 "m"_3)|`
= `|(0 - 3/(5 - x))/(1 + 0(3/(5 - x)))|`
tan θ = `|(3/(5 - x))/1|`
= `3/(5 - x)` ......(1)
tan ∠XAB = `|("m"_1 + "m"_2)/(1 + "m"_1 "m"_2)|`
tan(180° – θ) = `|(0 - 2/(1 - x))/(1 - 0 xx 2/(1 - x))|`
– tan θ = `|(2/(1 - x))/1|`
= `2/(1 - x)`
tan θ = `- 2/(1 - x)` ......(2)
From equations (1) and (2)
`3/(5 - x) = - 2/(1 - x)`
3(1 – x) = – 2(5 – x)
3 – 3x = – 10 + 2x
2x + 3x = 10 + 3
5x = 13
⇒ x = `13/5`
∴ The required point A is `(13/5, 0)`
APPEARS IN
संबंधित प्रश्न
Find the distance between the line 4x + 3y + 4 = 0, and a point (−2, 4)
Write the equation of the lines through the point (1, −1) perpendicular to 3x + 4y = 6
If (−4, 7) is one vertex of a rhombus and if the equation of one diagonal is 5x − y + 7 = 0, then find the equation of another diagonal
Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and through the point (−1, 2)
Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and parallel to x − y + 5 = 0
Find the equations of straight lines which are perpendicular to the line 3x + 4y − 6 = 0 and are at a distance of 4 units from (2, 1)
Find the equation of a straight line parallel to 2x + 3y = 10 and which is such that the sum of its intercepts on the axes is 15
If p1 and p2 are the lengths of the perpendiculars from the origin to the straight lines x sec θ + y cosec θ = 2a and x cos θ – y sin θ = a cos 2θ, then prove that p12 + p22 = a2
Find the family of straight lines parallel to 3x + 4y – 12
A line is drawn perpendicular to 5x = y + 7. Find the equation of the line if the area of the triangle formed by this line with co-ordinate axes is 10 sq.units
Find the image of the point (−2, 3) about the line x + 2y − 9 = 0
A photocopy store charges ₹ 1.50 per copy for the first 10 copies and ₹ 1.00 per copy after the 10th copy. Let x be the number of copies, and let y be the total cost of photocopying. Find the cost of making 40 copies
Find atleast two equations of the straight lines in the family of the lines y = 5x + b, for which b and the x-coordinate of the point of intersection of the lines with 3x − 4y = 6 are integers
Find all the equations of the straight lines in the family of the lines y = mx − 3, for which m and the x-coordinate of the point of intersection of the lines with x − y = 6 are integers
Choose the correct alternative:
The equation of the line with slope 2 and the length of the perpendicular from the origin equal to `sqrt(5)` is
Choose the correct alternative:
A line perpendicular to the line 5x − y = 0 forms a triangle with the coordinate axes. If the area of the triangle is 5 sq.units, then its equation is
Choose the correct alternative:
If the lines represented by the equation 6x2 + 41xy – 7y2 = 0 make angles α and β with x-axis then tan α tan β =
