Advertisements
Advertisements
प्रश्न
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and it passes through the point (5, 3). Find the co-ordinates of the point A
Advertisements
उत्तर
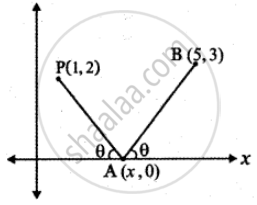
Let P(1, 2) and (5, 3) are the given points.
By the property of reflection,
∠XAB = ∠OAP = θ
(Angle of incidence = Angle of reflection)
Slope of the line OA(x – axis) m1 = 0
Slope of the line joining the points P(1, 2) and A(x, 0)
Slope of AP, m2 = `(2 - 0)/(1 - x) = 2/(1 - x)`
Slope of the line joining the points B(5, 3 ) and A(x, 0)
tan θ = `|("m"_1 + "m"_3)/(1 + "m"_1 "m"_3)|`
= `|(0 - 3/(5 - x))/(1 + 0(3/(5 - x)))|`
tan θ = `|(3/(5 - x))/1|`
= `3/(5 - x)` ......(1)
tan ∠XAB = `|("m"_1 + "m"_2)/(1 + "m"_1 "m"_2)|`
tan(180° – θ) = `|(0 - 2/(1 - x))/(1 - 0 xx 2/(1 - x))|`
– tan θ = `|(2/(1 - x))/1|`
= `2/(1 - x)`
tan θ = `- 2/(1 - x)` ......(2)
From equations (1) and (2)
`3/(5 - x) = - 2/(1 - x)`
3(1 – x) = – 2(5 – x)
3 – 3x = – 10 + 2x
2x + 3x = 10 + 3
5x = 13
⇒ x = `13/5`
∴ The required point A is `(13/5, 0)`
APPEARS IN
संबंधित प्रश्न
Show that the lines are 3x + 2y + 9 = 0 and 12x + 8y − 15 = 0 are parallel lines
Write the equation of the lines through the point (1, −1) parallel to x + 3y − 4 = 0
Write the equation of the lines through the point (1, −1) perpendicular to 3x + 4y = 6
If (−4, 7) is one vertex of a rhombus and if the equation of one diagonal is 5x − y + 7 = 0, then find the equation of another diagonal
Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and parallel to x − y + 5 = 0
Find the equations of two straight lines which are parallel to the line 12x + 5y + 2 = 0 and at a unit distance from the point (1, −1)
Find the equations of straight lines which are perpendicular to the line 3x + 4y − 6 = 0 and are at a distance of 4 units from (2, 1)
Find the length of the perpendicular and the co-ordinates of the foot of the perpendicular from (−10, −2) to the line x + y − 2 = 0
Find the family of straight lines perpendicular
A line is drawn perpendicular to 5x = y + 7. Find the equation of the line if the area of the triangle formed by this line with co-ordinate axes is 10 sq.units
Find the image of the point (−2, 3) about the line x + 2y − 9 = 0
Find atleast two equations of the straight lines in the family of the lines y = 5x + b, for which b and the x-coordinate of the point of intersection of the lines with 3x − 4y = 6 are integers
Choose the correct alternative:
The slope of the line which makes an angle 45° with the line 3x − y = −5 are
Choose the correct alternative:
The intercepts of the perpendicular bisector of the line segment joining (1, 2) and (3, 4) with coordinate axes are
Choose the correct alternative:
A line perpendicular to the line 5x − y = 0 forms a triangle with the coordinate axes. If the area of the triangle is 5 sq.units, then its equation is
Choose the correct alternative:
The point on the line 2x − 3y = 5 is equidistance from (1, 2) and (3, 4) is
Choose the correct alternative:
If a vertex of a square is at the origin and its one side lies along the line 4x + 3y − 20 = 0, then the area of the square is
Choose the correct alternative:
If the lines represented by the equation 6x2 + 41xy – 7y2 = 0 make angles α and β with x-axis then tan α tan β =
